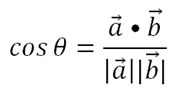Robot control software: Difference between revisions
| (39 intermediate revisions by 3 users not shown) | |||
| Line 7: | Line 7: | ||
*5. Push the object away | *5. Push the object away | ||
*6. Ask for help | *6. Ask for help | ||
*7. Wait for help | |||
*8. Helping other robot | |||
This behaviour has been visualized in the following flowchart: | This behaviour has been visualized in the following flowchart: | ||
| Line 44: | Line 46: | ||
The way the convertion of steps to distance and degrees is calculated, by using the tacho counter (rotationsensor of the actuator) , is shown below: | The way the convertion of steps to distance and degrees is calculated, by using the tacho counter (rotationsensor of the actuator) , is shown below: | ||
<math> | <math> D \quad = \quad T/35 </math> | ||
<math> Y = Y + (-T/35) | ''Where D is distance in centimeter and T is the rotation of the motor in degrees. | ||
<math> R \quad = \quad T \cdot (5/31)</math> | |||
''Where R is rotation in degrees and T is the rotation of the motor in degrees. | |||
The following formulas are used to update the robots location and direction, based on the values of the tacho counter: | |||
<math> X \quad = \quad X + (-T/35) \cdot \cos(F) </math> | |||
<math> Y \quad = \quad Y + (-T/35) \cdot \sin(F) </math> | |||
''Where T is the value of the tacho counter, and F is the angle between the robot and the x-axis.'' | ''Where T is the value of the tacho counter, and F is the angle between the robot and the x-axis.'' | ||
<math> F = F-(D | <math> F \quad = \quad F-(D \cdot \pi)/180 \quad mod \quad 2\pi </math> | ||
''Where F is the current angle between the robot and the x-axis, and D is the number of degrees the robot will turn.'' | ''Where F is the current angle between the robot and the x-axis, and D is the number of degrees the robot will turn.'' | ||
| Line 94: | Line 106: | ||
As described above, a robot will enter the "Going to Help" state when it is closest to the robot asking for help and has therefor received the coordinates and direction of the robot asking for help. | As described above, a robot will enter the "Going to Help" state when it is closest to the robot asking for help and has therefor received the coordinates and direction of the robot asking for help. | ||
When the robot comes in this state, it first calculates the coordinates it should go to, which is determined to be 20 centimeters behind the robot that is asking for help. It does this by using the received direction of the robot asking for help and using sine and cosine functions. These calculated coordinates will be referred to as the destination coordinates. | When the robot comes in this state, it first calculates the coordinates it should go to, which is determined to be 20 centimeters behind the robot that is asking for help. It does this by using the received direction of the robot asking for help and using sine and cosine functions. These calculated coordinates will be referred to as the destination coordinates. They are calculated as follows: | ||
<math> x_{destination} \quad = \quad x_{help} - 20 \cdot cos(f_{help})</math> | |||
<math> y_{destination} \quad = \quad y_{help} - 20 \cdot sin(f_{help})</math> | |||
''Where <math>x_{destination}</math> and <math>y_{destination}</math> are the x and y values of the destination coordinates respectively, <math>x_{help}</math> and <math>y_{help}</math> are the x and y coordinates of the robot asking for help respectively and <math>f_{help}</math> is the angle of the robot that is asking for help with respect to the x-axis. | |||
Next, the robot transforms its direction into a unit vector. It does this by taking the sine and cosine of the angle it is pointed in. This is done using the following formulas: | Next, the robot transforms its direction into a unit vector. It does this by taking the sine and cosine of the angle it is pointed in. This is done using the following formulas: | ||
<math>Fx = cos(F)</math> | <math>Fx \quad = \quad cos(F)</math> | ||
<math>Fy = sin(F)</math> | <math>Fy \quad = \quad sin(F)</math> | ||
''Where Fx and Fy are the x- and y value of the unit vector respectively and F is the angle of the robot with respect to the x-axis. | |||
The last two things the robot has to do is calculate the angle it should make from | Next, the robot computes the vector that goes from his own current position to the destination coordinates, calculated at the beginning of this state. | ||
This is done using the following two formulas: | |||
<math>x \quad = \quad x_{destination} - x_{own}</math> | |||
<math>y \quad = \quad y_{destination} - y_{own}</math> | |||
''Where x and y are the x and y values of the vector, <math>x_{destination}</math> and <math>y_{destination}</math> are the x and y coordinates of the destination respectively and <math>x_{own}</math> and <math>y_{own}</math> are the robot's own current x and y coordinates. | |||
The last two things the robot has to do is calculate the angle it should make from its current position to go in the direction of its destination coordinates and the angle it should make after it reaches its destination coordinates to align with the robot asking for help. These two angles will, from here on, simply be referred to as first and second angle respectively. | |||
The first angle is calculated using the dot product as shown in the following formula: | The first angle is calculated using the dot product as shown in the following formula: | ||
| Line 115: | Line 142: | ||
The only problem that occurred here was that the dot product calculates the sharpest angle between two vectors, but we programmed the robots to always turn left. This meant that whenever turning right would make the smallest angle, the robot would go in the wrong direction, as it would turn left. Therefore we also determine whether the robot should turn right or left. | The only problem that occurred here was that the dot product calculates the sharpest angle between two vectors, but we programmed the robots to always turn left. This meant that whenever turning right would make the smallest angle, the robot would go in the wrong direction, as it would turn left. Therefore we also determine whether the robot should turn right or left. | ||
The | The second angle is calculated by subtracting the angle of the robot coming to help by the angle of the robot asking for help, both with respect to the x-axis. | ||
The formula is as follows: | |||
<math> second angle \quad = \quad angle_{help} - angle_{self}</math> | |||
== Communication == | == Communication == | ||
| Line 137: | Line 167: | ||
The right route has been traveled and the robot is in location. It will follow the other robots until it is either out of bounds or the pressure sensor is being triggered. | The right route has been traveled and the robot is in location. It will follow the other robots until it is either out of bounds or the pressure sensor is being triggered. | ||
=== | === Send === | ||
In the send | In the send class three functions are defined: askLocations, help and arrived. | ||
* | *askLocations | ||
This function will try to connect to all available robots and send integer 0, after which te other robot will send their location and id which will be stored using a hashmap with robot id's for keys. | |||
*help | *help | ||
| Line 149: | Line 179: | ||
When a robot arrives after being called for aid it will send a message to the robot in need to make sure it knows both can start pushing. | When a robot arrives after being called for aid it will send a message to the robot in need to make sure it knows both can start pushing. | ||
== | == SRC Code == | ||
This .zip file contains the source code for the NXT robots: | |||
[[File:NXTSwarm.zip]] | |||
Back to: [[PRE2015_2_Groep1]]<br> | Back to: [[PRE2015_2_Groep1]]<br> | ||
Latest revision as of 23:20, 17 January 2016
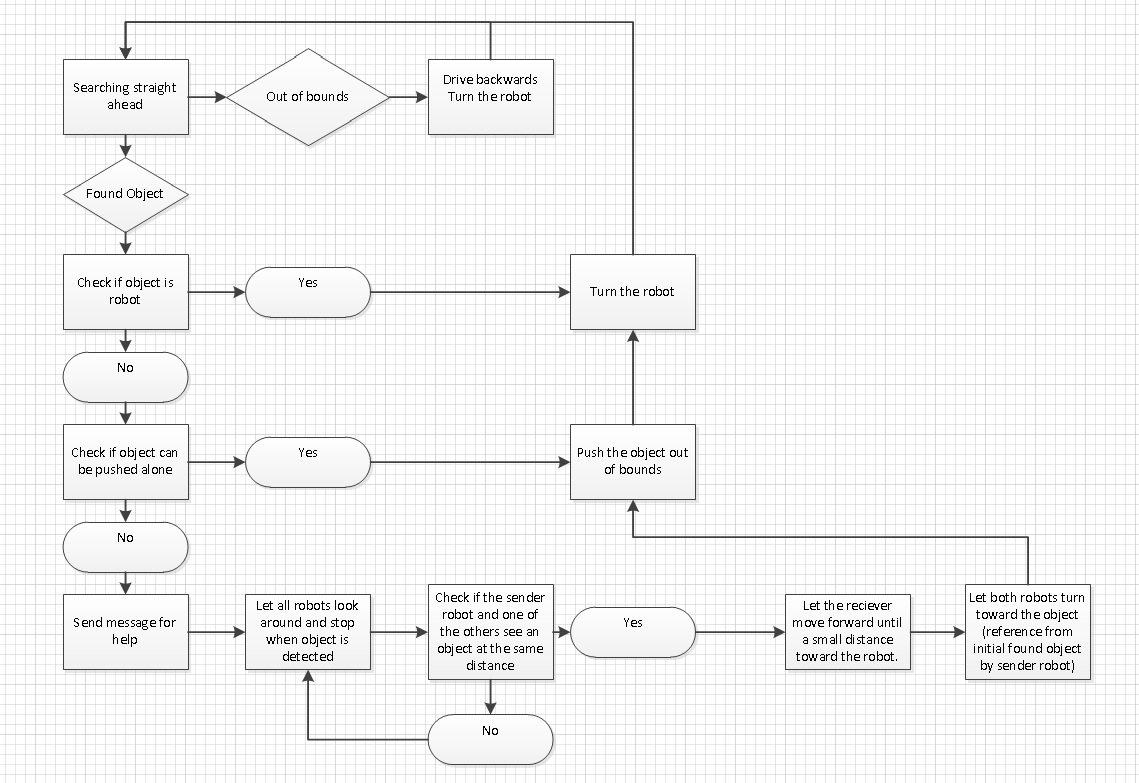
For the behaviour of the NXT Robots a state-based algorithm has been used. There are several main states in which te robot can be:
- 1. Searching straight ahead
- 2. Turning
- 3. Found something
- 4. Check if the object is too heavy
- 5. Push the object away
- 6. Ask for help
- 7. Wait for help
- 8. Helping other robot
This behaviour has been visualized in the following flowchart:
Localisation
The localisation of the robots is a very important part of the project. With localisation, the robot is able to keep track of its own position and direction. This is of high importance when a robot encounters a heavy object, because now it can find out which robot is the nearest to him and ask this specific robot for help. Besides the localisation, we use bluetooth to communicate between the robots.
Programming the Localisation
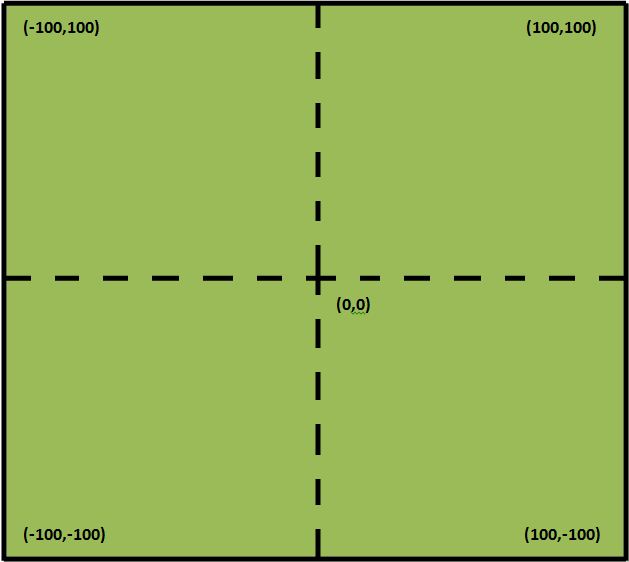
We created a square field in which the robots would be present the entire time. The center of the field would have the coordinates (0,0). Since the field is 2 x 2 meters and distance in the code is expressed in centimeters, the corners of the field have the following coordinates: (-100, -100), (100, -100), (100, 100) and (-100, 100). A schematic representation of the field is given:
The dotted lines are not present in the real world. They are in this schematic picture to clarify the (0,0) point in the field.
To begin, first the following information should be a given for the robot:
- Its beginposition (x- and y-coordinate)
- Its begindirection (angle of its direction with respect to the x-axis)
From this point on the rotation sensor inside of the actuators used for the NXT Robots are used to keep track of the robot's position. When the wheels of the robot are rotating, the robot is either going forward, going backwards or turning. This has to be taken into account when converting the steps of the motor to either angle or distance.
When the robot is going forward, the rotation sensor counts the steps that the actuator makes. These steps are then converted to a distance. To calculate this convergence factor, the robot was programmed to drive forward and continuously print the steps of the actuators on its display until the pressure sensors gave a value above zero. Next, the robot was placed at an exact distance of 1 meter from a heavy object. After hitting the heavy object the values of step was read and the convergence was calculated by dividing 100 by the amount of steps. This gave us the amount of steps per centimeter. This was done 3 times and the average value was exactly 35 steps. So in conclusion, from here the robots were able to drive a given straight distance with an inaccuracy of approximately 1 cm.
This same principle was used to establish the amount of steps per degree of turning. We entered an amount of steps (positive for one actuator, negative for the other) so the robot would start turning. This was done until the amount of steps for turning 360 degrees was known. After this the convergence factor from steps to degrees turned out to be 5/31.
From here we were able to make the robots go to any given position. However, an inaccuracy of approximately 5 degrees was found in the turning of the robots, due to slipping and the inaccuracy of the rotation sensors in the actuators themselves. This lead to the fact that when the robot was following a route, the inaccuracy of keeping track of its location, increased after every turn the robot made.
The way the convertion of steps to distance and degrees is calculated, by using the tacho counter (rotationsensor of the actuator) , is shown below:
[math]\displaystyle{ D \quad = \quad T/35 }[/math]
Where D is distance in centimeter and T is the rotation of the motor in degrees.
[math]\displaystyle{ R \quad = \quad T \cdot (5/31) }[/math]
Where R is rotation in degrees and T is the rotation of the motor in degrees.
The following formulas are used to update the robots location and direction, based on the values of the tacho counter:
[math]\displaystyle{ X \quad = \quad X + (-T/35) \cdot \cos(F) }[/math]
[math]\displaystyle{ Y \quad = \quad Y + (-T/35) \cdot \sin(F) }[/math]
Where T is the value of the tacho counter, and F is the angle between the robot and the x-axis.
[math]\displaystyle{ F \quad = \quad F-(D \cdot \pi)/180 \quad mod \quad 2\pi }[/math]
Where F is the current angle between the robot and the x-axis, and D is the number of degrees the robot will turn.
The Tachocounter is reset before it starts moving straight, backwards or starts turning. Also The robots will move straight ahead for the amount of 10.000 steps. This is a random high number. This means that the robots will move straight ahead until they end up in another state. Other states the robot could end up in are:
- The "Out of Bounds" state, where the robot has reached one of the borders of the field.
- The "Go to object" state, where the robot encounters an object.
- The *Asking for help" state, where the robot determines which robot is nearest to him and asks this robot to help him.
- The "Going to help" state, where the robot is on its way to another robot that needs help, pushing a heavy object out of the perimeter.
Out of Bounds State
Each robot is equipped with a light sensor that points to the ground. This light sensor is shown in the Figure below:
The area in which the robot should stay is set up with tape that has a different color than the surface the robots are driving on.
Whenever the light sensor of a robot detects the change of light intensity, caused by the tape, the robot will end up in the "Out of Bounds" state. Whenever the robot reaches the tape, it will go backwards for 30 centimeters and will then turn 120 degrees. After this the robot goes back to the first state in which it will drive straight again.
Go to Object State
Every robot is also equipped with an ultrasonic sensor which can detect objects. When this sensor detects an object within a distance of 40 centimeters, it will drive towards it. Then the following things happen:
- When the robot drives over the tape, it will return to the "Out of Bounds" state.
- When the robot encounters the object and the object is heavy enough to press in either the left or the right pressure sensor, the robot will go to the "Asking for Help" state.
- When the robot is asked for help before it has encountered the object it will go to the "Going to Help" state.
In short, this will make sure that when the object is light enough not to press in one of the pressure sensors, the robot will push the object out of the perimeter. When the object is so heavy it will press in one of the pressure sensors, the robot will ask for help and when the robot is asked for help by another robot before it encountered a heavy object, the robot will go and help the other robot instead.
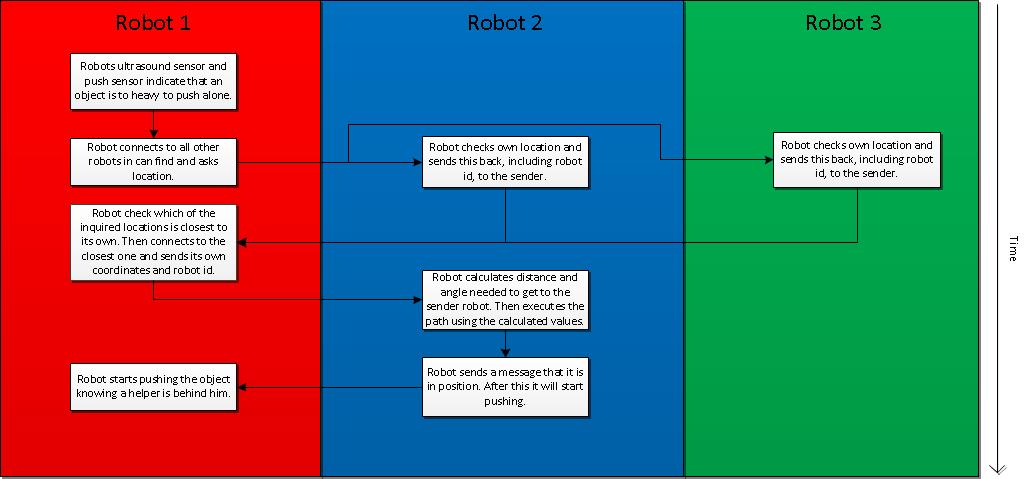
Asking for Help State
Whenever the robot is in this state, it means it has encountered an object which was heavy enough to press one or both of the pressure sensors. From here the robot will have to determine which robot is closest to him. To accomplish this, a working wireless communication system is needed and some vector calculations. The communication will be explained in section 2 on this page called "Communication". What happens when the robot ends up in the "Asking for Help" State, is that he will ask both robots to send him their current location. Then, knowing its own position and the position of the other robots, it is able to calculate the distance between itself and the other robots using the Pythagorean theorem. After the robot has determined which robot is nearest to him, he will send his own current location to that specific robot and stops driving.
Now the robot that has to come help has received the coordinates where it should go. From here it will enter the "Going to Help" state.
The process of the robot asking other robots for help is also shown in our video that can be viewed by clicking this link: https://youtu.be/i56Wzx9wmNc.
Going to Help State
As described above, a robot will enter the "Going to Help" state when it is closest to the robot asking for help and has therefor received the coordinates and direction of the robot asking for help.
When the robot comes in this state, it first calculates the coordinates it should go to, which is determined to be 20 centimeters behind the robot that is asking for help. It does this by using the received direction of the robot asking for help and using sine and cosine functions. These calculated coordinates will be referred to as the destination coordinates. They are calculated as follows:
[math]\displaystyle{ x_{destination} \quad = \quad x_{help} - 20 \cdot cos(f_{help}) }[/math]
[math]\displaystyle{ y_{destination} \quad = \quad y_{help} - 20 \cdot sin(f_{help}) }[/math]
Where [math]\displaystyle{ x_{destination} }[/math] and [math]\displaystyle{ y_{destination} }[/math] are the x and y values of the destination coordinates respectively, [math]\displaystyle{ x_{help} }[/math] and [math]\displaystyle{ y_{help} }[/math] are the x and y coordinates of the robot asking for help respectively and [math]\displaystyle{ f_{help} }[/math] is the angle of the robot that is asking for help with respect to the x-axis.
Next, the robot transforms its direction into a unit vector. It does this by taking the sine and cosine of the angle it is pointed in. This is done using the following formulas:
[math]\displaystyle{ Fx \quad = \quad cos(F) }[/math]
[math]\displaystyle{ Fy \quad = \quad sin(F) }[/math]
Where Fx and Fy are the x- and y value of the unit vector respectively and F is the angle of the robot with respect to the x-axis.
Next, the robot computes the vector that goes from his own current position to the destination coordinates, calculated at the beginning of this state. This is done using the following two formulas:
[math]\displaystyle{ x \quad = \quad x_{destination} - x_{own} }[/math]
[math]\displaystyle{ y \quad = \quad y_{destination} - y_{own} }[/math]
Where x and y are the x and y values of the vector, [math]\displaystyle{ x_{destination} }[/math] and [math]\displaystyle{ y_{destination} }[/math] are the x and y coordinates of the destination respectively and [math]\displaystyle{ x_{own} }[/math] and [math]\displaystyle{ y_{own} }[/math] are the robot's own current x and y coordinates.
The last two things the robot has to do is calculate the angle it should make from its current position to go in the direction of its destination coordinates and the angle it should make after it reaches its destination coordinates to align with the robot asking for help. These two angles will, from here on, simply be referred to as first and second angle respectively.
The first angle is calculated using the dot product as shown in the following formula:
Here vector "a" represents the robot's direction as unit vector. Vector "b" represents the vector that goes from the robot to its destination coordinates.
The only problem that occurred here was that the dot product calculates the sharpest angle between two vectors, but we programmed the robots to always turn left. This meant that whenever turning right would make the smallest angle, the robot would go in the wrong direction, as it would turn left. Therefore we also determine whether the robot should turn right or left.
The second angle is calculated by subtracting the angle of the robot coming to help by the angle of the robot asking for help, both with respect to the x-axis. The formula is as follows:
[math]\displaystyle{ second angle \quad = \quad angle_{help} - angle_{self} }[/math]
Communication
Asking for help will be done using a bluetooth communication protocol:
Bluetooth
Because the NXT robots use bluetooth communication and several other devices around use this aswell the robots were paired first to make sure it's mac adress inventory contained all the needed content. Whenever a robot has to send a message it will try to connect with one of the robots based on bluetooth-id. Because every robot runs a seperate thread continuously listening for pending bluetooth connections a connecting try to one of the robots will always result in a stable connection in which both robots can send and receive information. However, if another robot wants to send or receive information the current connection has to be terminated because only one connection at a time is possible.
Seperate Receiving Thread
As stated above a seperate thread was used continuously listening for pending connections. Based on the first integer received a certain case within this thread is triggered. In the receive thread three cases were used, one of which will be chosen according to the first integer received (0, 1 or 2) when a connection is established.
- 0
The robot checks in which state he is, according to this the integer 'busy' will either get a value 0 or 1. After this the robot will send it's bluetooth id, x location, y location, angle relative to the x-axis and busy value to the robot which tried to connect and send integer 0 first.
- 1
The robot is being asked for help and therefore needs to read the location of the other robot after which the robot will calculate the needed route to go for aid.
- 2
The right route has been traveled and the robot is in location. It will follow the other robots until it is either out of bounds or the pressure sensor is being triggered.
Send
In the send class three functions are defined: askLocations, help and arrived.
- askLocations
This function will try to connect to all available robots and send integer 0, after which te other robot will send their location and id which will be stored using a hashmap with robot id's for keys.
- help
When the shortest distance to both robots is calculated the help function will connect to the closest robot and sent it's own locations to it. This way the other robot can calculate the route to come for aid.
- arrived
When a robot arrives after being called for aid it will send a message to the robot in need to make sure it knows both can start pushing.
SRC Code
This .zip file contains the source code for the NXT robots:
Back to: PRE2015_2_Groep1