Steekproefomvang

Een belangrijk onderdeel van afnemen van een vragenlijst zijn de mensen die de vragenlijst invullen.

Om een betrouwbaar resultaat te krijgen moet je voldoende mensen ondervragen, belangrijke punten voor het bepalen van de steekproefomvang zijn:

niveau van nauwkeurigheid

het niveau van nauwkeurigheid ook wel steekproef error genoemd, zegt iets over de mate van waarheids getrouwheid de vragenlijst wordt ingevuld.

een grotere steekproefomvang zorgt voor een hoger niveau van nauwkeurigheid en dus een lagere error.

voor deze vragenlijst gaan we uit van een steekproef error van 5%.

Het vertrouwens level

Het vertrouwens level is gebaseerd op de centrale limit theorie, deze zegt dat als je maar vaak genoeg sampled de gemiddelde waarde naar de werkelijke waarde zal gaan.

ook zegt de gemiddelde afwijking van deze limit, de standaarddeviatie, iets over de betrouwbaarheid van de responsie. deste grooter de groep is die binnen de standaarddeviatie valt deste beter is je risico level.

een grotere steekproefomvang zorgt voor een hoger vertrouwen.

wij gaan uit van een vertrouwens level van 95%

Graad van variatie

De graad van variatie zegd iets over de diversiteit van je populatie, deste hoger je diversiteit is deste groter moet je steekproefomvang zijn.

Doordat wij ons op een leeftijdsgroep richten neem de diversiteit iets af, wel hebben we geen verdere selectie eisen dus onze groep zal nog steeds redelijk divers zijn.

De berekening

Om de omvang van een steekproef te bepalen zijn er meerdere mogelijkheden, de eerste mogelijkheid voor grote populaties is het gebruik van een formule:

[math]\displaystyle{ n =\frac {Z_{a/2}^2 \times p \times q}{e^2} }[/math]

met:

• n: de steekproef omvang
• Z: is een statistische waarde uit een tabel die de oppervlakte van een normale verdeling weergeeft. [math]\displaystyle{ Z_{a/2}^2 }[/math] is het oppervalkte van een curve die tot a loopt
• a: 1-a is het vertrouwenslevel
• p: de diversiteit
• q: 1-p
• e: graad van nauwkeurigheid

een andere, eenvoudigere manier is het aflezen uit een al bestaande tabel.

in tabel 1 van: http://www.soc.uoc.gr/socmedia/papageo/metaptyxiakoi/sample_size/samplesize1.pdf

is het vertrouwenslevel 95% en de diversiteit maximaal namelijk .5. dit kan overeenkomen met onze steekproef.

voor een error van 5% en een doelgroep van meer de 100.000 personen vinden we dan een steekproefomvang van 400 responsies

Responsie

bij het afnemen van een online vragenlijst zal niet reageren dus als je 400 personen de lijst stuurt zul je niet 400 responsies krijgen.

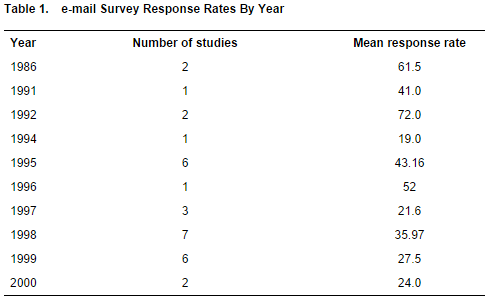
uit:E-mail Survey Response Rates: A Review ,Kim Bartel Sheehan 2006

als deze dalende lijn doorgezet heeft en we uitgaan van een responsie van 20%, dan moeten we 2000 personen benaderen.

op http://ctb.ku.edu/en/table-of-contents/assessment/assessing-community-needs-and-resources/conduct-surveys/main

hebben ze het zelfs over een responsie van slechts 2%. om deze responsie te verhogen moet men zich richten op het persoonlijker maken van de uitnodiging.

als we daadwerkelijk maar 2% halen moeten we 20.000 personen benaderen, dit is een erg grote groep.

bronnen:

http://www.soc.uoc.gr/socmedia/papageo/metaptyxiakoi/sample_size/samplesize1.pdf

http://hum.sagepub.com/content/52/4/421.full.pdf+html

http://onlinelibrary.wiley.com/doi/10.1111/j.1083-6101.2001.tb00117.x/full

http://www.socialresearchmethods.net/kb/sampterm.php

http://www.robertniles.com/stats/margin.shtml