Mobile Robot Control 2024 Ultron:Final Report

(Group deadline: 21:00 28 June)

Introduction

High-Level System Description

（Yidan)

System Architecture

State Flow

(Liz)

Data Flow

The data flow diagram illustrates the interactions between input sources, processing modules, and output commands for the robots. There are three major input sources: the laser and odometry come from the robot sensors, and the map is uploaded by the user. The map provides the existing representation of the restaurant environment, including the table positions and order information. The laser detects obstacles in the environment. The odometry supplies information regarding the robot’s position and velocity.

The Localization module first receives the data from all three inputs to determine the robot's position relative to the map. Over time, the robot's theoretical and actual positions will eventually diverge because of accumulated errors from odometry conversions between theoretical and real movement. Therefore, it’s fundamental to ensure that the robot knows its exact position within the environment during its movement for accurate navigation. The position is then forward to both Global Navigation and Local Navigation modules.

Global Navigation uses the map to plan an optimal path from the robot’s current position to the destination through the combination of PRM and A* algorithms and updates the current target point for Local Navigation. Local Navigation uses the current position, the target point, and the laser data to adjust the robot's path dynamically, avoiding obstacles and navigating through tight spaces. It provides control commands for linear and angle velocity to guide the robot's motion.

The Stuck Detection module handles abnormal status during the local navigation. If the robot is within 0.2 meters of an obstacle according to laser data or cannot find a path to reach its target points due to an unknown static obstacle or being stuck in a local minimum, the stuck detection module is triggered. It stopped the robot and initiated a path re-planning through the Global Navigation module.

The process involves a continuous feedback loop, constantly monitoring and adjusting the robot's movements based on inputs and environments to ensure safe and efficient navigation towards its destination.

System components

Initialization

(Lu)

Localization

（Aori）

Global Navigation

（Yidan, Hao）

A* search algorithm

The A* algorithm we implemented has two working modes: it can build a planner by obtaining connected nodes from the grid information or the PRM algorithm. Since the grid information of the map is not given in the final challenge, we use the sampling nodes and connections between nodes given by the PRM algorithm.

The idea of ​​building a path planner based on PRM is as follows:

1. Read the coordinates of the start and end points from the configuration file. If the configuration file contains start and goal parts, overwrite the default values.

2. Get the number of nodes and connections in PRM and create a new node list and connection relationship container. Copy the node and connection information in PRM to the new node list and connection relationship container. Node ID starts from 2, and 0 and 1 will be used for the start and end points.

3. Create the start and end nodes and add them to the node list. Check the validity of the connection between the start and end points and the existing nodes, and establish a connection relationship.

4. Planner creation and initialization, set the initial cost [math]\displaystyle{ g }[/math] of each node to infinity, the heuristic cost [math]\displaystyle{ h }[/math] to the Euclidean distance from the node to the goal node, and the total cost to [math]\displaystyle{ g + h }[/math]. Create an open list to store the nodes to be processed, initially including the start node. Create another closed list to store the processed nodes.

5. Start path planning and select the node with the smallest total cost value in the open list for expansion. If the node is the target node, the path is found and the loop ends. Otherwise, add the neighbor nodes of the current node to the open list and update their initial cost value, total cost value and parent node. Remove the current node from the open list and add it to the closed list.

6. Starting from the target node, trace back to the parent node and generate a path.

7. The return value of the planner contains the node list, connection relationship, start and end nodes.In the main program, the A* algorithm is called before the while loop and after the PRM call. By adding reasonable conditional judgments and printing content, we ensure that the nodes and connection content can be read from the generated PRM image results. In order to deal with the situation where the node connection generated by a certain call to the PRM algorithm is unreasonable due to improper PRM parameters and the randomness of PRM, and then A* has no solution output, we set the corresponding judgment conditions. In this case, PRM and A* are called again. Ensure that there is an executable node list in the final pass to the local navigator.

Local Navigation

Dynamic Window Approach

Given a target point by global navigation algorithm and positions of obstacle by laser sensor, local navigation aims to calculate an available path to avoid collision with the obstacles as well as to move towards the target point. The outputs of all local navigation algorithms shown in lectures are directly the desired velocities [math]\displaystyle{ (v, \omega) }[/math] ([math]\displaystyle{ v }[/math] is linear and [math]\displaystyle{ \omega }[/math] is angular velocity) of the robot. There is no need to perform a path following task.

In exercising, we implemented both Artificial Potential Filed (APF) Algorithm and Dynamic Window Approach (DWA). At first, we chose APF as our local navigation algorithm because of its robustness and simplicity. However, during the test we found that APF is not ideal for vertex handling and the robot will oscillate when driving through a corridor, whereas DWA can generate smoother trajectories and shows great potential for dealing with complex scenarios. And DWA is designed to deal with the constraints imposed by limited velocities and accelerations, because it is derived from the motion dynamics of the mobile robot. This is well suited to the realities of Hero. Moreover, DWA contains the idea of optimal control, which can improve the efficiency of the robot. Thus, we switched to DWA.

Distance between obstacles and trajectory

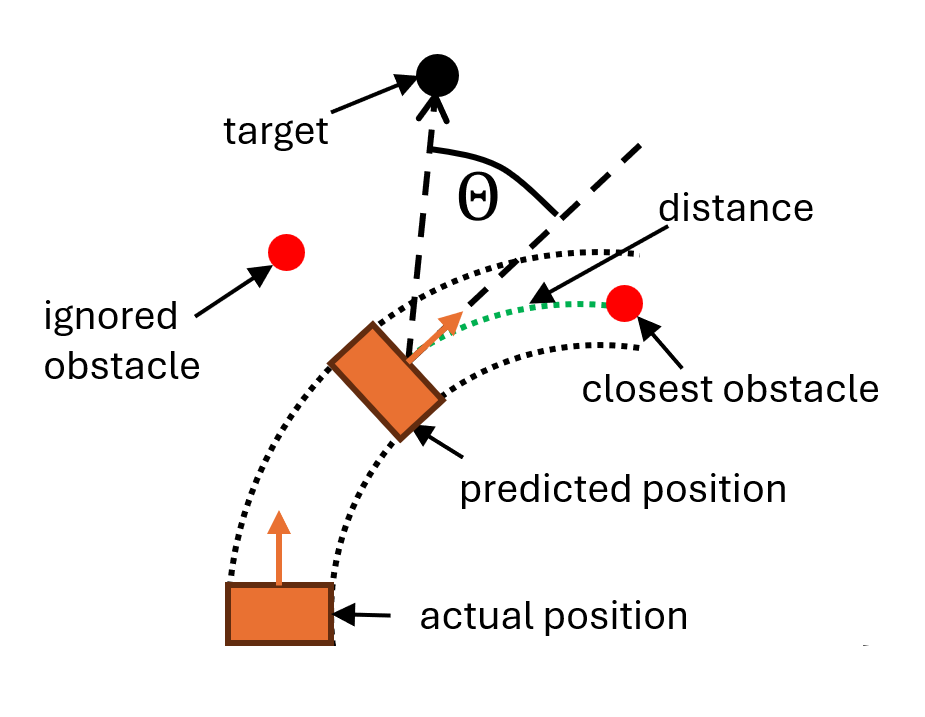
DWA performs reactive collision avoidance. When computing the next moving command, DWA considers only a short time interval, within which the robot's velocities [math]\displaystyle{ (v, \omega) }[/math] are considered to be constants. The algorithm will evaluate the results of all possible velocities and select the optimal one. Instead of using the simplified version introduced in lectures, we use the original version of this algorithm proposed by D. Fox, etc. The main difference is that the original algorithm uses a more refined geometric model when calculating the distance between the obstacle and the predicted trajectory, taking both the trajectory and the robot size into account. As shown in figure on the right, the obstacles that are not on the trajectory will be ignored. And by including a safety margin, we can control the minimum distance between obstacles and Hero.

The set of all possible velocities [math]\displaystyle{ V_r }[/math] is called the search space. It is the intersection of three sets: [math]\displaystyle{ V_r = V_s\cap V_a\cap V_d }[/math], where [math]\displaystyle{ V_s }[/math] is the set of velocities that are limited by robot's dynamics, [math]\displaystyle{ V_a }[/math] is the set of velocities with which the robot can stop before reaching the closest obstacle and [math]\displaystyle{ V_d }[/math] is the set of velocities constrained by current velocities and acceleration.

These three sets are defined as:

[math]\displaystyle{ \begin{align} \begin{matrix} V_s =&\left\{v,\omega |v\in[v_{min},v_{max}]\wedge \omega\in[\omega_{min},\omega_{max}] \right\}\\ V_a =&\left \{v,\omega |v\le \sqrt{2d(v,\omega )\dot{v}_b } \wedge \omega \le \sqrt{2d(v,\omega )\dot{\omega }_b} \right \}\\ V_d =&\left \{v,\omega |v\in [v_{a}-\dot{v}\Delta t,v_{a}+\dot{v}\Delta t] \wedge \omega \in [\omega_{a}-\dot{\omega}\Delta t,\omega_{a}+\dot{\omega}\Delta t] \right \} \end{matrix} \end{align} }[/math]

where [math]\displaystyle{ \dot{v}_b }[/math] and [math]\displaystyle{ \dot{\omega }_b }[/math] are maximum deceleration values and [math]\displaystyle{ d(v,\omega) }[/math] is the distance to the closest object; [math]\displaystyle{ v_a }[/math] and [math]\displaystyle{ \omega_a }[/math] are actual velocities and [math]\displaystyle{ \dot{v} }[/math] and [math]\displaystyle{ \dot{\omega} }[/math] are maximum acceleration values.

[math]\displaystyle{ V_s }[/math] and [math]\displaystyle{ V_d }[/math] ensure that the selected reference velocities is consistent with the physical limitations of the robot. And [math]\displaystyle{ V_a }[/math] ensures that the robot does not collide, because the distance item of velocities that lead to collision will be zero, making these velocities unavailable.

Implementation in C++

Pseudo code of DWA

As shown in the figure on the right, the DWA is basically a discrete search to maximize the reward function. Considering the large number of parameters of DWA, we implement DWA as a class in C++ and make those parameters as class-scope private constants. There are two advantages to such an implementation.

Firstly, with the limitation of class scope and constant private variables, these parameters will not be accessible to other code, which guarantees these parameters will not be modified by other code and helps to improve code clarity.

Secondly, packaging all the parameters of DWA in a single class helps to improve the portability of the code. One can easily use this code by including a head file. And if we want to change these parameters only, we can simply re-compiler this part solely and then link it with others, instead of re-building the whole project. The reason we didn't use a file (such as JSON or XML) to configure these parameters is that we want the compiler to perform compile-time constants optimization, as these parameters should be known constant in the final challenge.

Parameter Tuning

Simulation Results

Test on Hero

Interaction

When the robot reaches the target table location, it turns in the direction of the table and performs voice interaction. This function is realized as follows.

1.Checking if the Robot is Near the Table

We set variables like flag_table_0 are defined in the code to indicate whether the task of reaching a table is complete. If flag_table_0 is true, it means the task is not yet completed. Later, it calculates the distance between the robot's current position and the target position. If this distance is less than the predefined threshold distance, it determines that the robot is near the target.

2.Updating the Flag and Outputting Information

Upon detecting that the robot is near the table, the code sets flag_table_0 to false to indicate that the task has been completed, preventing the code from executing the same task again. It then outputs the current value of flag_table_0 to the console, which is mainly used for debugging purposes to confirm that the flag has been correctly updated.

3.Calculating the Target Angle

The principle for calculating the angle the robot needs to rotate is as follows: First, calculate the direction angle towards the target table by using the difference between the target table's position and the robot's current position (using the atan2 function). Then, determine the angle the robot needs to rotate by calculating the difference between the robot's current orientation and the target direction angle.

4.Rotating the Robot

To make the robot face the table, the code enters a while loop that continues until the absolute difference between the current angle and the target angle is less than 0.01 radians. Inside the loop, the code outputs a message indicating that the robot is turning and sends a rotation command to the robot with a speed of 0.3 radians per second. It reads new odometry data to update the robot's pose, ensuring the angle data is up-to-date. The loop repeats this process until the robot's current angle is close enough to the target angle.

5.Stopping the Rotation and Reporting Arrival

Once the robot reaches the target angle, the code outputs a message indicating that the robot has arrived at the table. It sends a command to stop the robot's rotation and makes the robot speak to report that it has arrived at the table.

Final Challenge Results

Results Analysis

（Hao）

Until the final challenge, we did not successfully integrate the localization code, so we used the backup code in the final challenge. The code only includes the local navigator of DWA and the global navigator using PRM and A*. And added the following functions: update the robot position information according to the Odometry data, determine whether it has reached the table position based on the position information, turn on the spot after reaching the table, make the robot face the table, and give a clear arrival prompt. Then return to the original direction and use the local navigator to go to the next table. Repeat the above steps for any table until you reach the end of the node list given by the global navigation.

In the first round of robot testing, we did not successfully reach the first table because the actual starting position of the robot did not match the map position specified in the config file. The actual position was to the left of the ideal specified position, which caused the first table to cross the robot's global navigation trajectory. It encountered obstacle avoidance behavior generated by local navigation at the first table, which also prevented it from getting close to the table position we specified to determine the location. The judgment condition for the table position is a one-time flag and a real-time calculation of the Euclidean distance between the current position and the specified table position. Therefore, the wrong robot starting position made the subsequent path and table position judgment invalid. The robot always believed that it had not reached one of the node lists, so it tried to return by turning at a large angle and reach the coordinate position corresponding to that node. However, since the node coordinates are in the actual table position, the robot cannot reach them, so the first attempt was not successful. The video can be checked in

In the second attempt, we adjusted the robot's starting position and gave instructions to control movement during normal program operation, but the robot did not move. We were later told by the TA that this was due to an unknown robot hardware failure. Therefore, we were given a third attempt.

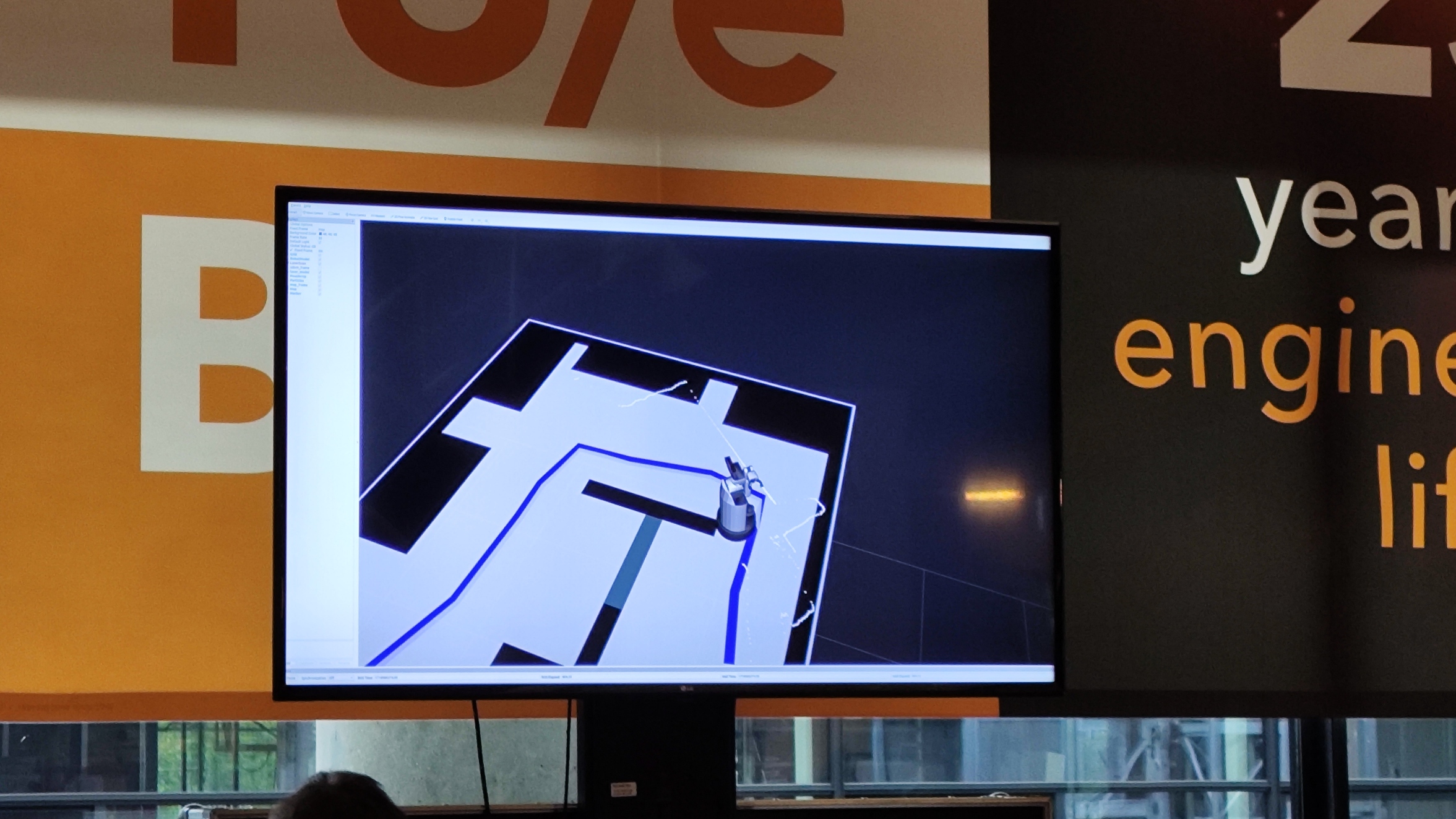
In the third attempt, after rigorous distance measurement, we used the relatively correct actual robot starting coordinate position. After calling PRM and A* global navigation, the robot generated a node list and provided it to the DWA algorithm to perform local navigation, track each node and refresh the node according to the list. After a period of straight tracking, we arrived near Table 0. When the Euclidean distance condition and the one-time flag judgment condition were both met, the "reaching the table" program was entered. The robot stopped on the spot and rotated 90 degrees to the left on the spot to make the robot face the dining table. The robot gave an obvious arrival prompt sentence "I arrived at table zero", then stopped for 5 seconds, rotated 90 degrees to the right on the spot, and the program returned to the normal tracking state. The robot went to Table 1. In the final challenge, it was not necessary to reach Table 1, so we blocked the flag for Table 1 and would not enter the execution state of Table 1. There is also a chair as an obstacle in the vicinity of Table1. The obstacle partially passes through the node coordinates generated by global navigation. Here, the DWA algorithm takes effect and helps the robot avoid the chair. After passing Table 1 and crossing the obstacle, the robot continues to move toward Table 2, and the arrival state for Table 2 is also triggered near Table 2. The arrival state content of Table 2 is as described in Table 0 above. When the robot returns to the normal tracking state after executing Table2, we find that the robot's return rotation angle does not match the robot's rotation angle to face Table 2. This is because the ground is slippery and the odometry method has errors in the cumulative calculation of angles. As the robot travels more distance, the odometry self-addition calculation method will inevitably have errors in coordinate information and angle information, and the errors will gradually increase. We did not use the localozation method, so this problem is inevitable. This results in the robot thinking that its position and orientation do not match the actual position and orientation of the robot, and we have no ability to correct this error. In the visual interface, we can clearly notice that the laser data's detection of the surrounding walls no longer matches the shape characteristics of the surrounding walls in the map interface, with a deviation of more than 45 degrees, as the picture shows on right. This error causes the robot to think that the coordinate information of the nodes on the path appears in the wall, which cannot be solved by local navigation or global navigation. The robot cannot reach the coordinates of the next node, resulting in the node being unable to update, and finally the robot does not reach Table 4. Only after reaching Table 4 will it enter the state of looking for Table 3 and "requesting to open the door." Therefore, the subsequent states cannot be achieved.

The summary of the Final Challenge is as follows:

1. The robot needs to set an accurate actual starting position, which strictly complies with the coordinate information and orientation information provided by the config file. This can be ensured by manual measurement of the actual map. If the robot's starting position deviates, it will cause the map information and global navigation trajectory information to deviate, which will affect the deviation of the robot's actual map motion trajectory.

2. Since localization is not used, a carefully designed config file and initial and final coordinate information must be provided to the robot for global navigation. The robot coordinates and orientation information must be calculated using the self-addition method of odometry.

3. Odometry calculations will continue to accumulate coordinate information errors, which will increase as the robot travels farther. This phenomenon will be exacerbated if the robot is running on a slippery surface or making frequent turns. This will eventually lead to unreliable coordinate information. We didn' see this error in simulation but it is vital fot real robot test.

4. The Table judgment condition we provide for the robot relies heavily on the Euclidean distance calculation between a specified coordinate position and the current robot position. If the robot's current position is wrong, the robot cannot correctly enter the state of reaching the Table.

Future Improvement

（Nan）