Mobile Robot Control 2024 Ultron:Final Report: Difference between revisions
Tag: 2017 source edit |
|||
| Line 25: | Line 25: | ||
[[File:Distance between obstacles and trajectory.png|thumb|right|Distance between obstacles and trajectory]] | [[File:Distance between obstacles and trajectory.png|thumb|right|Distance between obstacles and trajectory]] | ||
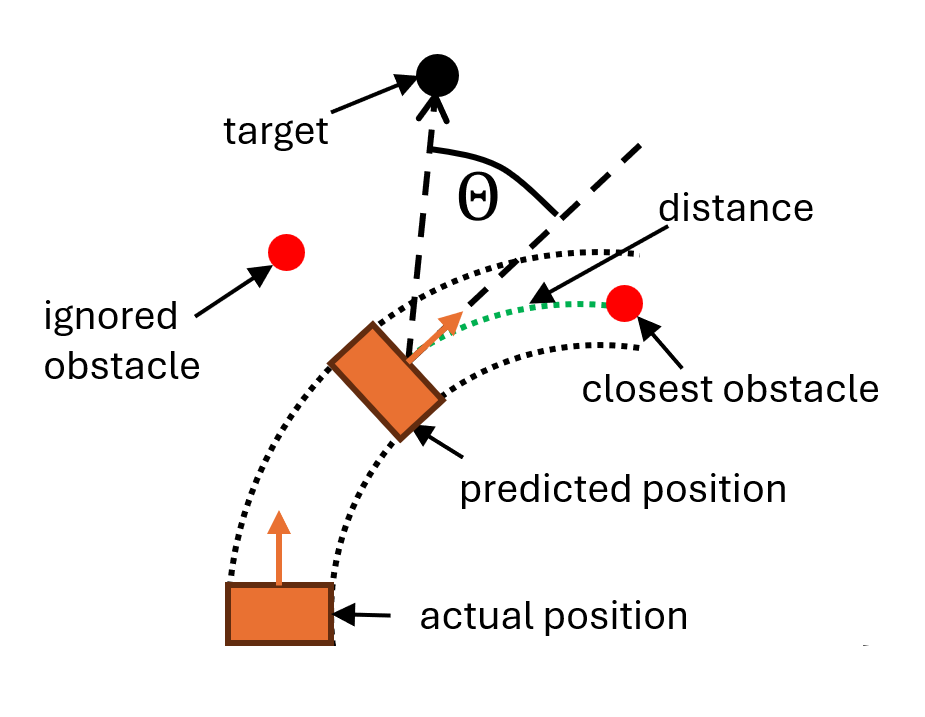
DWA performs reactive collision avoidance. When computing the next moving command, DWA considers only a short time interval, within which the robot's velocities <math>(v, \omega)</math> are considered to be constants. The algorithm will evaluate the results of all possible velocities and select the optimal one. Instead of the simplified version introduced in lectures we use the original version of this algorithm proposed by D. Fox, etc<ref>D. Fox, W. Burgard and S. Thrun, "The dynamic window approach to collision avoidance," in ''IEEE Robotics & Automation Magazine'', vol. 4, no. 1, pp. 23-33, March 1997, doi: 10.1109/100.580977. keywords: {Collision avoidance;Mobile robots;Robot sensing systems;Orbital robotics;Robotics and automation;Motion control;Humans;Robot control;Motion planning;Acceleration},</ref>. The main difference is that the original algorithm uses a more refined geometric model when calculating the distance between the obstacle and the predicted trajectory, taking both the trajectory and the robot size into account. As shown in figure on the right, the obstacles that are not on the trajectory will be ignored. | DWA performs reactive collision avoidance. When computing the next moving command, DWA considers only a short time interval, within which the robot's velocities <math>(v, \omega)</math> are considered to be constants. The algorithm will evaluate the results of all possible velocities and select the optimal one. Instead of using the simplified version introduced in lectures, we use the original version of this algorithm proposed by D. Fox, etc<ref>D. Fox, W. Burgard and S. Thrun, "The dynamic window approach to collision avoidance," in ''IEEE Robotics & Automation Magazine'', vol. 4, no. 1, pp. 23-33, March 1997, doi: 10.1109/100.580977. keywords: {Collision avoidance;Mobile robots;Robot sensing systems;Orbital robotics;Robotics and automation;Motion control;Humans;Robot control;Motion planning;Acceleration},</ref>. The main difference is that the original algorithm uses a more refined geometric model when calculating the distance between the obstacle and the predicted trajectory, taking both the trajectory and the robot size into account. As shown in figure on the right, the obstacles that are not on the trajectory will be ignored. | ||
==== Implementation in C++ ==== | ==== Implementation in C++ ==== | ||
Revision as of 15:59, 27 June 2024
(Group deadline: 21:00 28 June)
Introduction
High-Level System Description
(Yidan)
System Architecture
State Flow
(Liz)
Data Flow
(Liz)
System components
Initialization
(Lu)
Localization
(Aori)
(Yidan, Hao)
Dynamic Window Approach
Given a target point by global navigation algorithm and positions of obstacle by laser sensor, local navigation aims to calculate an available path to avoid collision with the obstacles as well as to move towards the target point. The outputs of all local navigation algorithms shown in lectures are directly the desired velocities [math]\displaystyle{ (v, \omega) }[/math] ([math]\displaystyle{ v }[/math] is linear and [math]\displaystyle{ \omega }[/math] is angular velocity) of the robot. There is no need to perform a path following task.
In exercising, we implemented both Artificial Potential Filed (APF) Algorithm and Dynamic Window Approach (DWA). At first, we chose APF as our local navigation algorithm because of its robustness and simplicity. However, during the test we found that APF is not ideal for vertex handling and the robot will oscillate when driving through a corridor, whereas DWA can generate smoother trajectories and shows great potential for dealing with complex scenarios. And DWA is designed to deal with the constraints imposed by limited velocities and accelerations, because it is derived from the motion dynamics of the mobile robot. This is well suited to the realities of Hero. Moreover, DWA contains the idea of optimal control, which can improve the efficiency of the robot. Thus, we switched to DWA.
DWA performs reactive collision avoidance. When computing the next moving command, DWA considers only a short time interval, within which the robot's velocities [math]\displaystyle{ (v, \omega) }[/math] are considered to be constants. The algorithm will evaluate the results of all possible velocities and select the optimal one. Instead of using the simplified version introduced in lectures, we use the original version of this algorithm proposed by D. Fox, etc[1]. The main difference is that the original algorithm uses a more refined geometric model when calculating the distance between the obstacle and the predicted trajectory, taking both the trajectory and the robot size into account. As shown in figure on the right, the obstacles that are not on the trajectory will be ignored.
Implementation in C++
Parameter Tuning
Simulation Results
Test on Hero
Interaction
(Lu)
Final Challenge Results
Results Analysis
(Hao)
Future Improvement
(Nan)
- ↑ D. Fox, W. Burgard and S. Thrun, "The dynamic window approach to collision avoidance," in IEEE Robotics & Automation Magazine, vol. 4, no. 1, pp. 23-33, March 1997, doi: 10.1109/100.580977. keywords: {Collision avoidance;Mobile robots;Robot sensing systems;Orbital robotics;Robotics and automation;Motion control;Humans;Robot control;Motion planning;Acceleration},