Mobile Robot Control 2020 Group 10

Team members:

Arend-Jan van Noorden (1378147)

Sjors Boutkan (0938234)

Jeroen van Meurs (0946114)

Koen van Gorkom (0954964)

Friso Buurman (0906665)

Escape Room

Design Document

The design document of group 10 can be found here.

Strategy

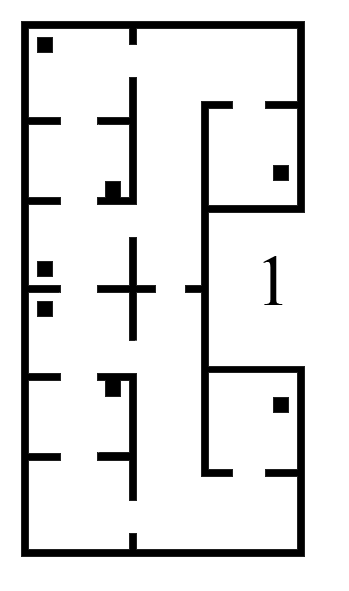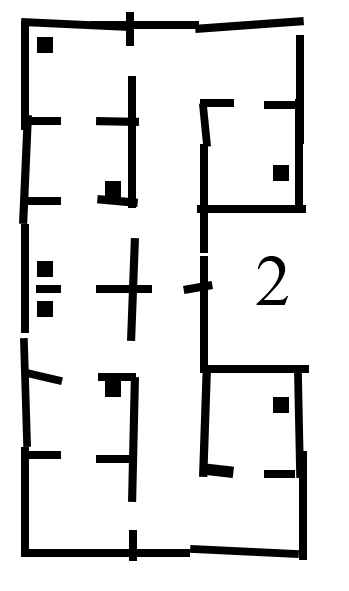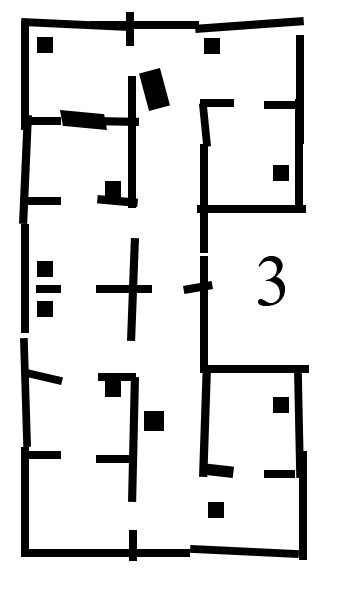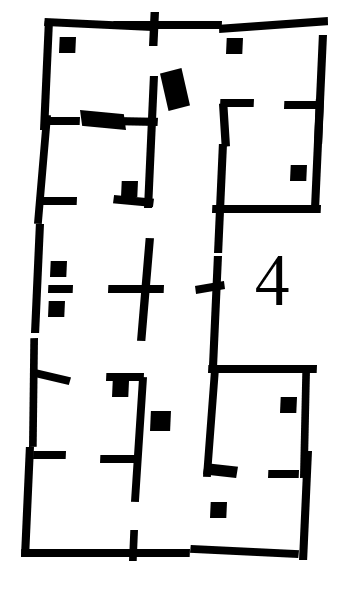
Solving the escape room is quite simple: find the corridor and drive through it. This document givesan overview of the system being build to solve this task.Finding the corridor is done by detecting the two outside corners marking the start of the corridor.Since the room is square, no other outside corners will be present in the environment. If these cornerscan’t be found from PICO’s initial location, it’ll follow the walls of the rooms clockwise, until thecorridor (outside corners) are encountered. The corresponding state diagram is shown in Figure1.1. The movement and navigation will be done using set-points and a potential-field algorithmpreventing PICO from hitting any obstacles or walls.

Requirements and Specifications

Links between requirements, functions and specifications.

Requirements	Specifications
PICO should not bump into walls	PICO's measurements are 0.41 m in width by 0.35 m in length
	The free radius around PICO should be at least 0.21 m
PICO cannot exceed speed limits	Maximum translational velocity is 0.5 m/s
	Maximum rotational velocity is 1.2 rad/s
Since PICO will be autonomous, it should be aware of its surroundings.	PICO should have an accurate map of its surroundings.
	LRF range is between 0.01 m and 10 m.
	LRF FOV is from -2 to 2 rad, measured over 1000 points of equal increments.
PICO should terminate when the final objective is reached.	PICO should come to a stop after it has crossed the finish line.
PICO should reach the final objective as soon as possible.	PICO should cross the finish line within 5 minutes.
PICO should not end up in a live lock state.	PICO should not keep repeating one action for over 30 seconds.
PICO should not end up in a dead lock state.	Careful coding has to be done to have no dead lock states.

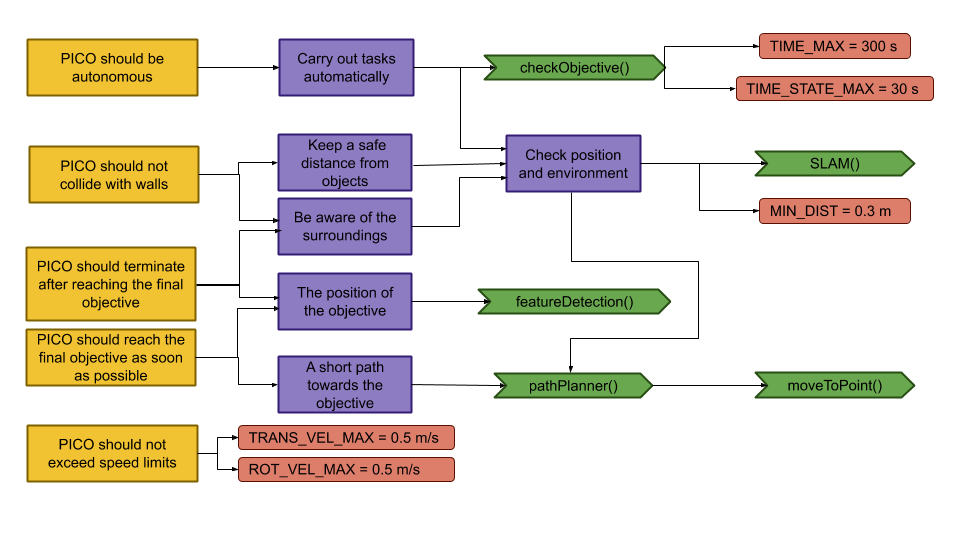
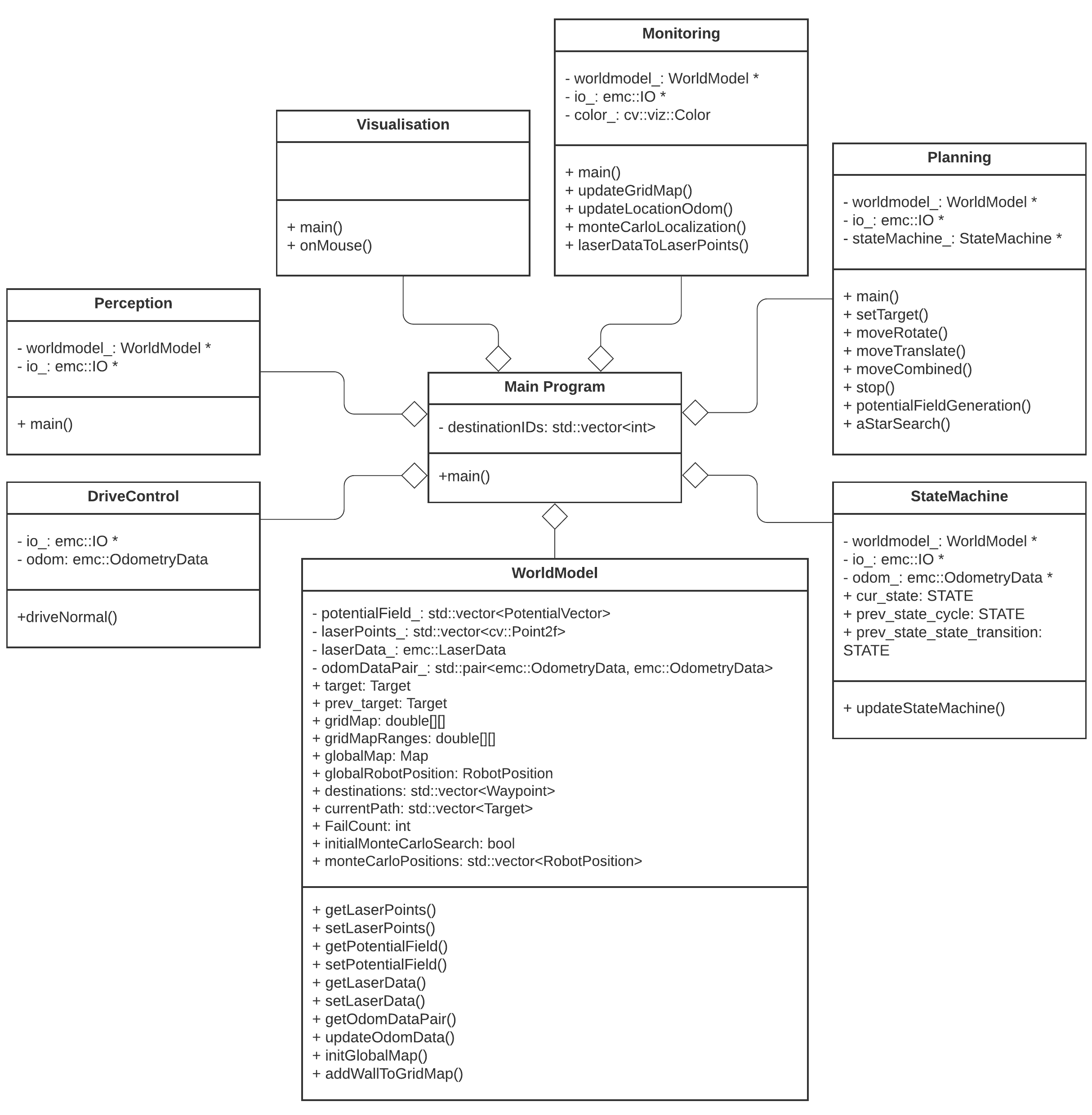
Components and Functions

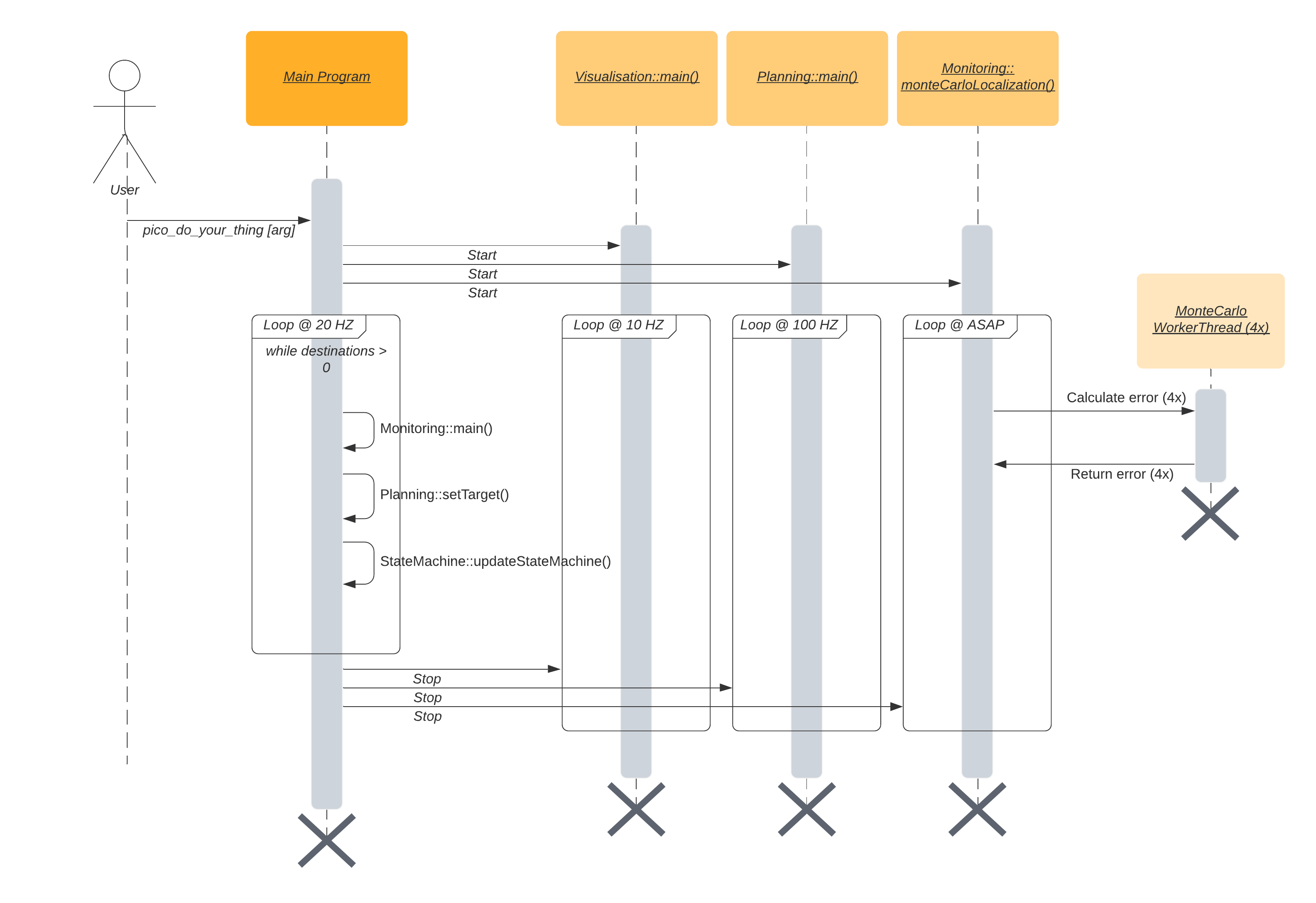
Basic architecture of robot code:

State machine of the control strategy for the maze challenge.

All functions need to be run based on a Finite State Machine. As with sensors, all data has noise so these data streams need to be filtered.

The tasks of each component can be divided in several functions each with a specific subroutine.

World model

The world model stores the information gathered by the components and distributes this information to the other components. The information consists of:

• A map of the surrounding area.
• A list of found features.
• The current and previous state.
• The next position to travel to.

The world model contains no functions because the world model is only used to store the world data, so there are no active subroutines present.

Plan

The plan component uses data from the world model to determine the next position PICO needs to go to. It thereby also check if the objective is met.

• checkObjective()
  The checkObjective function is the supervisor of the complete system. It controls/executes the states as defined in figure \ref{fig:state-machine} and executes the strategy as described in \ref{sec:strategy}. It will also check for failure of the system by identifying incorrect states, e.g. not moving for a set amount of time, following a wall for too long or having made a complete loop of the room without finding the corridor.

• pathPlanner()
  The plan component contains the path-planner function, this functions is responsible to define the setpoints for PICO. These setpoints will be determined based on the state machine and the world model.

Control

The control component makes sure PICO moves along the planned path.

• moveToPoint()
  The move to point function will be used to move PICO to the set point generated by the path planner. To prevent that PICO will hit the wall, the world model will be used to determine the trajectory from the current position of PICO to the set point.

Monitoring

The monitor component will try to identify features from the world model data.

• featureDetection()
  To determine the corners and walls of the maze the feature detection function will be used based on the world model data.

Perception

The perception component will gather the sensor data, clean it and update the world model with it.

• getLaserData()
  To acquire the data points of the laser sensor, the get laser data function will be used. The gathered data will be preprocessed to filter out the disturbances. The processed data will be written to the world model.

• getOdomData()
  The odometry date will be read out with the getOdomData function. This date will be written to the world model.

• SLAM()
  The gathered data from the laser and odometry sensors will be used to generate a map of the environment using Simultaneous Localization and Mapping (SLAM)

• UpdateVisuals()
  A window will be opened that shows all the detected features and the path that PICO is going. This function will update that window

Interfaces

All components interface with the world model, getting data required for their functions and setting data created to be used by other components. The world mode is the central data store. This can also be seen in figure Figure Boven. Differences between the the proposed system and the system originally shown in , is that there are no interfaces between the 'resources' and 'capabilities' and the world model. The world model will not be able to get it's own data or control the motors of the system. The interface to the sensors will be through the perception component and the controlling of capabilities will be done by the control component.

Challenge result

Sadly we did not manage to get out of the escape room, below we will discuss why and how we solved it.

Main

After the Maze challenge we analyzed which part of the main program caused the failure which lead to the the wall collision. The problem occurred in the corner detection function, which resulted in the interpretation of a inside corner as an outside corner. The planning algorithm used this corner as target position to search a second outside corner, and let the robot drive to this corner. With the absence of a potential field algorithm, the robot was able to drive through the wall.

The main program for the maze challenge is using the state machine as shown in the Components and functions paragraph, in the following paragraphs is the robot behavior at each state described.

• ORIENTING

In the first state the robot will turn to check if it can see a door or a outside corner. A door is defined if there are two outside corners within 0,5 m and 1,5 m from each other, or a outside corner and a wall within the same range as with the outside corners. If the robot is not able to find a door from its initial position, then there will be searched for a single outside corner. When there is no door or outside corner found then the robot will search for the closest wall to follow.

• SEARCH_FORWARD

If the robot cannot detect any features in the orienting state, then the robot will drive straight forward in the same direction as the initial orientation.

• ALIGN_TO_WALL

When multiple walls are detected the closest wall is determined, the angle between the wall and the robot will be computed to determine the rotation direction. When the robot is aligned within +/- 3 degrees the state will be set to FOLLOW_WALL.

• FOLLOW_WALL

The robot will follow the wall at 20 cm distance till a door or outside corner is found, if this is the case the state will be set to GOTO_DOOR or SEARCH_DOOR. Otherwise the robot will follow the wall if a second wall in front of the is found, when this second wall is closer by then the first wall the ALIGN_TO_WALL state will be called again.

• SEARCH_DOOR

If one outside corner is found a way point will be set 25 cm from the x and y direction with respect of the corner, with this way point there can be guaranteed that the robot will not collide with the wall. When the robot is at this position and the second outside is still not found it will to ORIENTING again, otherwise the robot will be set GOTO_DOOR.

• GOTO_DOOR

When the door is found the planning script will place a way point 25 cm in front of the midpoint of the door, if the robot is at this location the robot will be set to the DRIVE_THROUGH_DOOR state.

• DRIVE_THROUGH_DOOR

In this state the robot will drive to the way point 25 cm in the middle the door, when the robot loses the door the DRIVE_THROUGH_CORRIDOR state is set.

• DRIVE_THROUGH_CORRIDOR

To complete the maze a way point is set in the middle of the furthest corridor walls nodes. To determine the corridor walls there is checked if the walls are parallel to each other, if the perpendicular distance is between the 0,5 m and 1,5 m and if at least two wall nodes can be projected on the other wall to check if the walls are not after each other. When the robot is at this way point the robot has exited the maze and the state will be set to COMPLETED. Below there is shown that the robot is executing SEARCH_DOOR, GOTO_DOOR and DRIVE_THROUGH_CORRIDOR.

Backup

The maze challenge backup attempt. The current state of the state machine is visible in the picture.

The backup was a simple wall following algorithm. Initially, Pico will drive forwards until it encounters an object in front. Next, Pico will turn 90 degrees to the right. Then, as long as Pico's left side is obstructed, the wall will be followed while making adjustments to align with the wall and not strafe too close to the wall or too far away from the wall. Again, when the front is obstructed as well, Pico will turn 90 degrees to the right and the next wall will be followed. When a gap at the left side is detected, Pico will move forward a little bit, turn left and drive forward into the corridor. If the senses a object in front, Pico will know the opening was only a small gap and not the corridor, in this case Pico will rotate right and continue following the wall.

Unfortunately, the backup attempt failed as well. The problem Pico encountered during the challenge was an edge case which unfortunately did not result in a correct execution of the algorithm. After finding a wall at the front, Pico turned 90 degrees to the right. After the turn all sides were 'free', meaning that Pico thought he was next to a corridor. After turning left it noticed that its front was free and its left side was not. This triggered the state machine to believe it was in the corridor. When the state machine enters this state, the only possible state is the finished state. So after driving through the wall, all sides of Pico were 'free' again thus entering the finished state. Pico drove through the when it thought it was in the corridor. This is because of the specific laser beams that Pico uses for the collision detection. Pico checks three sides, using ten laser beams per side. The front side is the actual front of Pico. The right and left side however, are about 45 degrees from the front instead of 90. Since the actual side of Pico was not monitored, Pico thought he was still some distance away from the wall.

After the challenge a little time was spend to improve the behavior of the wall following algorithm. To this end, the hard 90 degree turns have been replaced by an alignment check and the collision detection was changed that the actual right and left side of Pico are measured. When an obstructing in front is detected, Pico rotates until the obstruction is not visible anymore and the left side is aligned to a wall. This is checked by comparing the ranges of a subset of the of the LRF to the left of Pico. When the ranges are about equal, Pico is aligned. With this improvement, Pico was able to reach the actual finish of the Maze Challenge.

Hospital challenge

Strategy [Sjors]

A robust strategy is required in order to complete the hospital challenge. The robot must be able to navigate through the hospital as smooth and fast as possible, while dealing with both static and dynamic clutter, wheel slip, offset walls and noise on all sensors, without using a pre-determined path. This requires solid building blocks for the code. These challenges are tackled in different ways, and are split up in multiple components.

[#World model|World model]] is used to store the information of the map and the sensors in two maps, a global map and a live map. The information is read from and written to this world model.

Planning is used in order to plan an optimal path through the map, which can change when clutter or closed doors are encountered.

Control focuses on the actuation of the robot itself.

Monitoring is a big component which takes all the perception data, and uses it to determine the position of the robot, the live map, and ???

Perception is the component which translates the raw sensor data to usefull information.

Statemachine is the brain component of the robot, and decides which steps need to be undertaken in order for the robot to complete its task.

The User interface is used in order to visualize the maps, the robot and its behavior, and can give tremendous insights during testing and execution of the tasks at hand.

Components [Friso]

The program written has been designed in a way it contains multiple, semi-independent, components all working together. Some of these even work in parallel to improve qualitative performance. In the following sections, these different components and their interactions will be dissected and explained. Below, the different components and their most important member attributes and methods.

UML Class diagram of the program

World model [Koen]

The world model is used as a database. This database is separated into two maps: A global map and a grid map. All gathered data is stored in the world model and then can be used by other processes. Besides the data structure the world model also has a couple of functions to update the model and extract data from it. The main function is "initGlobalMap", this is the initialization of the global map. Then the function "addWallToGridMap" is used to update the gridmap with all the statics walls. These functions will be described further below. Next to those main functions there are some smaller functions to update or extract odometry data,laser data, robot position and more.

Small portion of the global map. With wall described by the green lines, cabinets by the orange lines, the front of the cabint by the red lines and waypoints by the blue circles

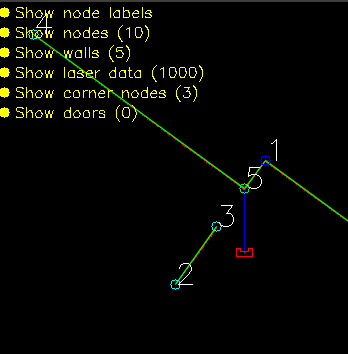
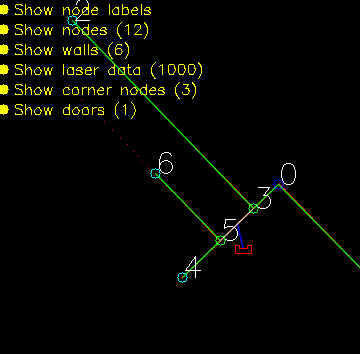
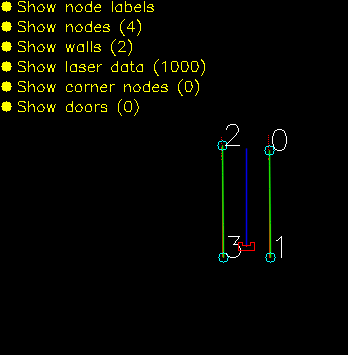
initGlobalMap This function loads a modified json and turns into into a global map as seen in picture **. Th json file consists of nodes, walls, cabinets and waypoints in front of the cabinets. Every item in this list will be visualized, this is done to make debugging easier. This global map is used as a reference base of the grid map and used to make a clearer visualization.

addWallToGridMap This function is used to create the basic grid map. It will use the walls that are supplied by the global map to fill in the grid map. This gives a solid base for a initial path planning.

Planning

The planning is made up of two major components: Target determination and path planning. The target determination is done based on the different states Pico can be in. During all states, but the "GOTO_NEXT_WAYPOINT", "ARRIVED_AT_WAYPOINT", "TRANSLATE_TO_WAYPOINT" and "APPROACHING_CABINET" states, the target is set to the current robot position to ensure the robot does not move. During the "PLAN_PATH" state, the A* algorithm is called to plan a new path to the next destination. During the "GOTO_NEXT_WAYPOINT" and "ARRIVED_AT_WAYPOINT" states, the target coordinates are set by the coordinates of the next waypoint on the current path. If the waypoint is reached, it is removed from the current path and the next waypoint is set as the target. During the "TRANSLATE_TO_WAYPOINT" the target is a predetermined waypoint just in front of a cabinet. When this waypoint is reached the state switches to "APPROACHING_CABINET" and the target is set such that Pico moves forward slowly.

Path Planning

For the path planning the A* algorithm is used. The A* algorithm is an informed search algorithm, meaning that it calculates the path based on weighted graphs or gridmaps. A* determines which of its paths to extend based on the cost of the path and an estimate of the cost required to extend the path all the way to the goal. In mathematical terms, A* selects the path that minimizes:

[math]\displaystyle{ f(x) }[/math] = [math]\displaystyle{ g }[/math]([math]\displaystyle{ x }[/math]) + [math]\displaystyle{ h }[/math]([math]\displaystyle{ x }[/math])

Where [math]\displaystyle{ x }[/math] is the next node on the path, [math]\displaystyle{ g }[/math]([math]\displaystyle{ x }[/math]) is the cost of the path from the start node to [math]\displaystyle{ x }[/math], and [math]\displaystyle{ h }[/math]([math]\displaystyle{ x }[/math]) is a heuristic function that estimates the cost of the cheapest path from [math]\displaystyle{ x }[/math] to the goal.

The heuristic function is the Euclidian distance between [math]\displaystyle{ x }[/math] and the goal, this means that the heuristic function is admissible. In other words: A* is guaranteed to return the least-cost path from start to goal.

The cost function [math]\displaystyle{ g }[/math]([math]\displaystyle{ x }[/math]) is based on the grid map generated from laser data. If a laser can is reflected at a grid point, the grid point is eventually flagged as blocked. A blocked grid point has a high integer value and a unblocked grid point has a value of zero if it is not close to a blocked grid point. The closer a unblocked grid point is to a blocked grid point, the higher the integer value of the grid point, thus also the higher the cost. To end up with the shortest path, the grid point values are raised by one and multiplied by one if [math]\displaystyle{ x }[/math] is a direct neighbor of the current node and multiplied by √2.

A* has some conditions which determine whether it is possible for a path to be planned. The simplest two are that the starting node and the goal node have to be reachable, meaning that their grid points are not flagged as blocked. The other condition is that there is a free path between the start node and the goal node. This free path in this implementation is a dynamic factor. To ensure that Pico does not collide with static objects, the grid map contains a certain range around blocked grid point where the values of the grid points are higher than zero. For the first iteration of the definition of a free path is that there is a unbroken line of grid points (diagonal counts as well) with a value of zero. This implies that Pico stays well away from all objects. If Pico cannot find a free path after the first iteration, the threshold of accepted grid point values is raised to incorporate the first row of grid points which is effected by a blocked grid point. The threshold keeps decreasing if no path is found until all grid points, except for the blocked grid points, are used by A*. If a path is found, the threshold is reset to its initial value.

Control

The control of Pico is made up of two components: An artificial potential field and a function which determines the different velocities that are fed into Pico's base.

Artificial potential field

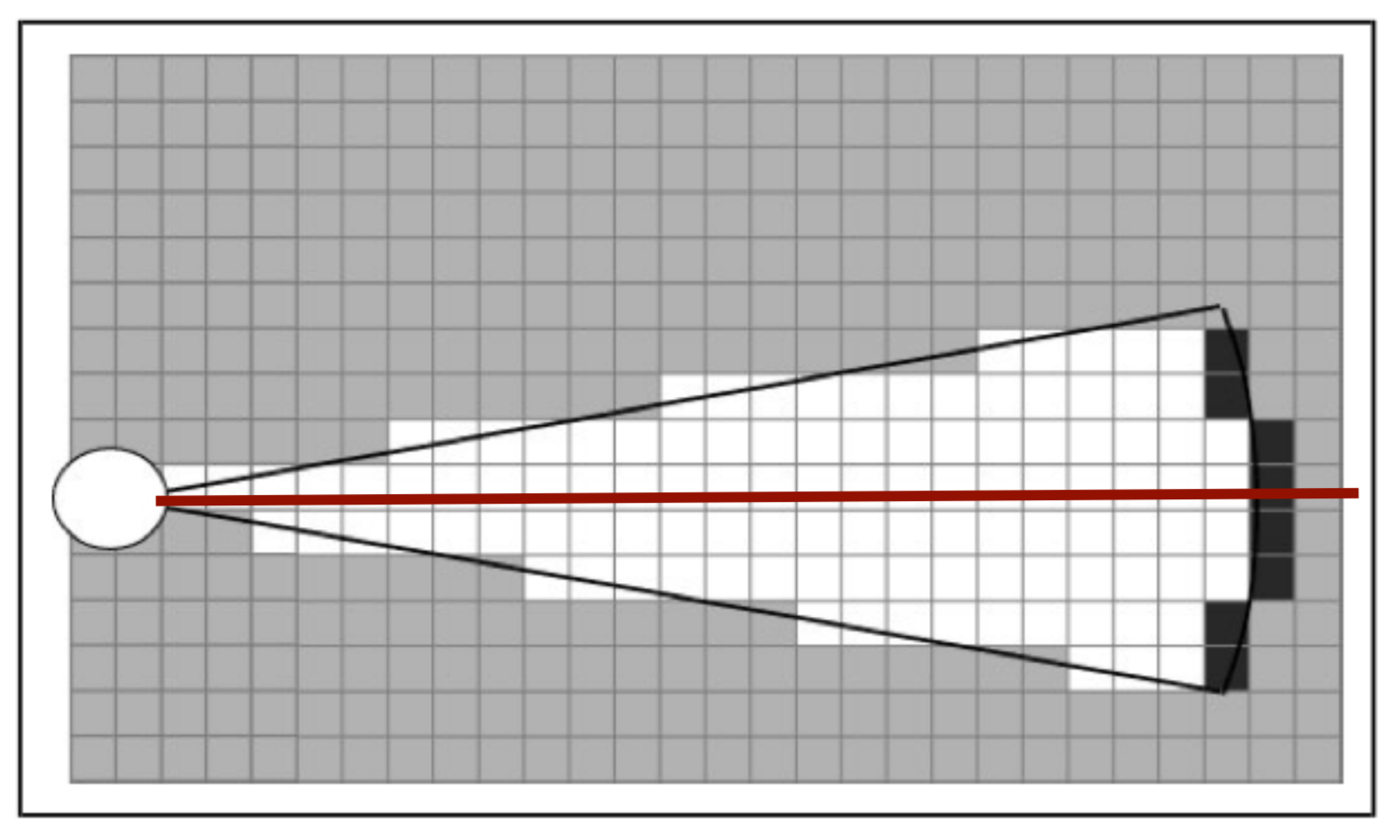
The path planning already accounts for a large deal of the obstacle avoidance, but it is not perfect on its own. Furthermore, the path planning is limited to planning a path around static objects. Any dynamic object is not picked accounted for in the gridmap used for the path planning. To solve these issues it is opted to use an artificial potential field, APF in short. The philosophy of the artificial potential field approach can be described as follows:

The manipulator moves in a field of forces. The position to be reached is an attractive pole for the end effector and obstacles are repulsive surfaces for the manipulator parts.

In this case, the position to be reached is the next path point. Since the APF is only used as a last resort for obstacle avoidance, we do not want the full effect of it at all times. To this end, the effect of the APF will only be exploited when Pico sees an obstacle within a certain range. At this particular range, the repulsive potential vector starts to increase from zero.

The repulsive potential vector is created from the live laser data Pico gathers at all times. If a laser beam has a range between the minimal range of the LRF and a maximum free distance around Pico, a vector is calculated in the following manner:

Need to insert formula's

Here [math]\displaystyle{ \eta }[/math] is a constant to scale the magnitude. [math]\displaystyle{ k }[/math] is a value to change the slope of the magnitude, higher values for [math]\displaystyle{ k }[/math] give a steeper slope. [math]\displaystyle{ D }[/math] is the distance between the robot and the laser point, or effectively the range of the laser beam. [math]\displaystyle{ \Delta }[/math] is the safe distance around Pico, for values of [math]\displaystyle{ D }[/math] higher than [math]\displaystyle{ \Delta }[/math] nothing will happen. The other way around the magnitude will increase. Finally laserPoint is the point in the local robot coordinate frame where the laser beam is reflected by an object.

Every laser beam results in an Vec_r. To final repulsive vector used in the actual control of the robot is the summation of all Vec_r. In this way vectors from adjacent sides are able to cancel each other.

For the final implementation of the APF only the repulsive vector is used. The vector to the next path point is taken as the attractive vector. Only when there is a repulsive vector with a magnitude greater than zero, so when there is an object within a distance [math]\displaystyle{ \Delta }[/math] from Pico, the repulsive vector is added to the attractive vector to act as a collision avoidance measure. To ensure that Pico will never run into any object, the APF is updated at an increases rate of 100 Hz. It is chosen to do this at a higher rate, since lower rates like 20 Hz would induce a oscillation if Pico was blocked by objects on two different sides, eventually leading to a collision.

A downside of the APF approach is the existence of local minima in which one could get stuck. For this implementation the local minimum does not really cause any problems, since the solutions are accounted for by other parts of the code. For instance, when a new object is detected on the current path of Pico, a new path is calculated. If Pico does find itself in a narrow situation, the path planning is optimized to find the best path possible within the boundaries provided by Pico.

Monitoring [Friso]

The monitoring component has the job of tracking and updating the robot's current position and it's surroundings. This class consists of two main parts: mapping of the robot's actual surroundings (incl. static clutter) and determining the exact position of the robot within the given global map using laser data. Mapping the surroundings is done using 'Occupancy Grid Mapping' and localization using laser data has been accomplished by implementing so called Monte Carlo localization.

Occupancy grid mapping (static clutter detection) [Friso]

To be able to create correct and efficient paths through the hospital, the robot has to be in possession of a complete and actual map of it's surroundings. This is done using Occupancy Grid Mapping. In this technique, a gridmap is drawn over the (given) global map, with each grid-square containing a single value indicating whether or not that grid-square is occupied (traversable) or not.

Populating the gridmap

Populating the gridmap is done once at program startup and then updated every main-program cycle. During initialization and interpretation of the given .json-map, the each grid-square being crossed by a wall or cabinet is assigned a value of GRID_WALL_VALUE (100.0).

During the execution of the program, the grid-squares' values are updated using the currently seen laserpoints. For each laserpoint, the corresponding grid-square in which it's located is determined and this grid-square's value is increased by GRID_LASER_BLOCKED_VALUE (0.5). Even more, the grid-squares positioned in between the robot's current location and the laserpoint's position are determined as being empty and have their values subtracted by GRID_LASER_FREE_VALUE (0.5). This uses the fact the robot wouldn't have been able to see an object if the grid-squares in between the object and the robot are not empty. Determination of which grid-squares are in between the robot and the laserpoint is done using a Bresenham algorithm implementation from tech-algorithm.com.

The ability to 'open up' grid-squares after they have been determined as being occupied, either by the initializing sequence or object detection, is crucial in creating a robust system being able to handle the imperfect world. E.g. dynamic clutter, doors or walls being in a slightly different position w.r.t. the given .json-map, being able to fix the gridmap after populating it with incorrect data due to an error in localization, etc.

Image showing example situation in which black squares are identified as being occupied and white squares are visibly unoccupied. Gray squares are currently out of view

Demonstration of the algorithm detecting closed doors and other clutter as soon as those are in view. First showing only actually occupied grid-squares, afterwards also showing the gradient around these grid-squares, which is used in path planning

Interpreting the grid-map

Since the gridmap consists of a collection of grid-squares, all possessing a value, this value has to be translated to a portion of the map being occupied or free. This is done by checking if the grid-square's value is above GRID_LASER_FREE_VALUE (0.5), if so, the grid-square should be interpreted as being occupied. This is done e.g. in the visualizer and in the planning of the path of the robot.

Preparing the gridmap for path planning use

The path planning algorithm (A*) does not use the 'raw' gridmap as described above. Instead, it uses a processed copy (gridMapRanges) which adds a region of obstruction around the detected objects with values tapering off the further away from this object. It normalizes all grid-square values to the range [0, 255]. These values are used by A* in a way it'll prefer staying away from objects but still being able to do so if absolutely necessary. The exact workings of A* and it's using of these grid-square values can be seen at the 'Planning & Control' section on this page.

For each grid-square which has been identified as occupied (grid-square value > GRID_LASER_FREE_VALUE), the grid-squares present in a circle of GRIDMAP_RESOLUTION * 6 (0.5 * 6) around the occupied grid-square are affected and have a value between 0 and 255 assigned to them. This is done using the following formula, in which [math]\displaystyle{ x }[/math] is the distance of the grid-squarew.r.t. the occupied grid-square diveded by GRIDMAP_RESOLUTION.

-std::pow((x*2),2) - x * 10 + 255

Monte Carlo localization [Friso]

Monte Carlo localization is used in order to determine the position of the robot within the map. Due to the initial position of the robot being roughly known and the ability to track the (rough) position of the robot using odometry data, this method is a relatively easy way to get an exact position whilst being relatively robust.

In this approach, a group of different robot positions is generated and a estimation is made on how well the current observations (laser points) fit each possible position. The one most likely to be the correct position is then chosen. The different steps of this process are explained below.

Generation of Monte Carlo positions

Possible new positions of the robot (Monte Carlo positions) consist of a position (x- and y- coordinates) and an orientation (angle). These positions are generated in a radius around the current robot position. The orientation of these positions are taken from a normal distribution around the current robot position's orientation. The exact way of calculating these values is related to the 'uncertainty' value of the current robot position. The higher this value, the greater the radius of the circle in which the positions are generated, the standard deviation of the normal distribution used and the amount of positions generated. This has two reasons:

1. If uncertainty is low, the amount of Monte Carlo positions generated can be minimized to reduce computational intensity and, in turn, runtime
2. If uncertainty is low, the same amount of positions can be distributed along a smaller area and orientation range. This can improve accuracy of the found position

This uncertainty value gets increases over time and is reset once a new position is determined using Monte Carlo. The new value is related to how much the robot has moved since the previous time the position has been determined using Monte Carlo. This uncertainty value is used in the generation of the Monte Carlo positions which are going to be checked.

Monte Carlo localization determining the initial position of the robot using a rough initial estimate. The green arrow represent the Monte Carlo positions tried.

Selecting the best Monte Carlo position

For each position, the likelihood of the position being the actual robot position has to be determined. This is done by calculating an 'error' value for each position. This is done by going through the currently seen laserpoints (with a position w.r.t. the robot), placing these points within the global map using the Monte Carlo position and determining the distance to the closest wall or cabinet. These distances are summed for all laserpoints and together make up the error value. The position with the lowest error value (in effect, the position in which the seen laserpoints line up with the given .json-map the best) is selected as a new robot position candidate. A last check is done to verify the found position is within reason (it's not unreasonably far away from the current position) and if so, it's set as the new robot position and the new position uncertainty is set.

Perception [Koen]

The perception module reads out the laser and odometry sensor data and writes it to the world model.

Statemachine [AJ]

RESET

ORIENTING

PLAN_PATH

GOTO_NEXT_WAYPOINT

ARRIVED_AT_WAYPOINT

FINISHED_PATH

ORIENTING_TO_CABINET

TRANSLATE_TO_WAYPOINT

APPROACHING_CABINET

ARRIVED_AT_CABINET

COMPLETED

This state is reached when all cabinets have been visited. The robot shuts down when this state is reached.

NONE

User interface [Koen]

Global map interface. With on the top left the menu to toggle the visualization of different parts of the map. On the top right are the runtimes shown of the different threads. On the bottom left is the toggle to turn on manual control

The main function of the interface is to show the current state of the robot in the world and what it will do next. This information can be used to more efficiently debug the code. The interface is created by the visualization scrip. This component uses the information from the world model to visualize the map. The information that is visualized can be adapted by activating or deactivating various parts, this can be done either in the code or on the visualized map itself. The interface has also the option to turn on manual control, this way it is easy to test specific positions of the robot.

e

x

t

r

a

v

e

r

t

i

c

a

l

s

p

a

c

e

Testing [Sjors & AJ]

The robot must the thoroughly tested before the final challenge. The robustness of all components must be tested and changed if needed in order to be sure that the robot can handle unexpected situations during the hospital challenge. Three main points have been tested in order to assure robustness: Imperfect maps, clutter objects and path planning obstacles.

Imperfect maps

Different versions of the hospital map were used during testing. The difficulty of the maps was increased over time, in order to tackle different aspects seperately. The .json file, which gives a perfect map of the hospital lay-out is given, which was used during the first stages of testing. It must be noted that this 'perfect' version of the map is not sufficient for testing purposes. The imperfect maps have been created in order to test the robustness of the robot. The added imperfections include holes in the walls, offset walls and cabinets, and skewed maps. The different stages of the imperfect maps are shown in the Figure below.

The first custom test map contains multiple gaps between walls, as well as misplaced wall segments. This simulates the real enviromnment, where different imperfections are present.

The second custom map includes extra static clutter. The static clutter is placed at key positions where the robot normally would drive in order to complete its tasks. The path planning of the robot, as well as the way it deals with extra clutter objects is tested using this map.

The third map includes a large skew angle. The bottom part of the map stays relatively close the original map, while the top of the map has a big offset. The overall error regadring misplaced segments therefore increases vertically. This allowed the use of 1 map for an increasing amount of error. The robot was first tested at the bottom half of the map. When it was concluded that the robot could handle the small errors at the bottom of the map, the robot was tested at the top half of the map, which proved to be more difficult.

Different test maps used during testing. 1) The perfect .json map. 2) Uneven walls with gaps and misplaced wall segments. 3) Multiple extra pieces of clutter. 4) Skewed map by over 3 degrees with respect to the vertical.

Eventhough the walls were not perfectly aligned with the .json map, the robot had little problems navigating through the map. The grid map in combination with the potential field ensured that the robot would not run into walls, even when walls were completely in the wrong place.

An exceptional case in which the robot would fail to navigate through the hospital is when the walls are offset so much that the combination of the seen walls and the predetermined locations of the walls block the entire path. This unique case would require a huge difference between the .json map and the simulation map. It is therefore assumed that this would not be the case during the final challenge.

The localization in skewed maps also proved to be difficult. If the initialization and localization at the start fail, and have a rotational offset, the robot got lost with no way of getting back on track. This problem was solved by changing the conditions and the thresholds of the first initialization. Once the position was well established the robot was allowed to continue.

Dijkstra's algorithm shown on an old map. An obstruction has been placed between waypoint 8 and 9

Path planning

A different path planning strategy was used in the early stages of the project. This strategy used manually set waypoints throughout the map, and Dijkstra's algorithm to navigate through these waypoints. The links between the waypoints can be made inactive if an obstruction on the path of the robot is observed. Though this strategy was promising, it was eventually discarded in favor of the gridmap and A* approach. This choice was made based upon robustness. A lot of manual waypoints must be placed in order to ensure that the robot can drive through the hospital with all kinds of different clutter configurations. This way of 'hard coding' the path also seemed like a rather messy solution.

Clutter

The addition of static clutter was handeled very well by the robot. The gridmap proved to be an excellent tool for this, since every small piece of obstruction can now be tracked and taken into account when planning a path. The dynamic clutter was added in the same fashion, but the removal of previously occupied grid spaces was not finely tuned. This would result in a large smear of occupied grid spaces caused by a dynamic object. After fine tuning the parameters, the dynamic clutter was robustly taken care of by the robot