Mobile Robot Control 2024 Ultron:Final Report: Difference between revisions
Tag: 2017 source edit |
|||
| (4 intermediate revisions by one other user not shown) | |||
| Line 87: | Line 87: | ||
===Localization=== | ===Localization=== | ||
Localization is a critical component in the final challenge to ensure accuracy of actual position in the map during navigation. Given the random initial pose and accumulating error over time when solely using odometry data to calculate the pose, the localization module corrects the robot's position using sensor data and a map of the environment. | Localization is a critical component in the final challenge to ensure accuracy of actual position in the map during navigation. Given the random initial pose and accumulating error over time when solely using odometry data to calculate the pose, the localization module corrects the robot's position using sensor data and a map of the environment. | ||
In localization module, particle filter algorithm is utilized based on the following procedure: A set of particles is initialized across the map, each representing a possible position of the robot. Each particle is assigned an initial weight and uniformly distributed. As the robot moves, each particle’s position is updated based on odometry data, which includes some randomness to account for motion noise. Then, it uses sensor data to perform measurement update, each particle’s weight is updated based on how well the data matches the expected laser data from that particle’s position. Particles have better match gets higher weights. Multinomial Resampling method is used to resample a new set of particles by drawing with replacement from the current set of particles, with the probability of drawing a particle proportional to its weight. This step helps focus the particles around the more probable positions and discards particles with low weights. Finally, the robot’s estimated position is determined by the weighted average or the most likely particle position based on the current set of particles. | |||
We have tested the localization component individually in physical setup and the map is identical with the final challenge map. Firstly, a initial position was given to the Hero robot within specified region according to final challenge requirements. The tests involved starting from different initial pose and the result indicates that the particle converges quickly and the map inferred from estimated position align well with the actual final challenge map. The video tape of the individual test are shown in the link below. | |||
[https://youtu.be/eCI-Purs5BE individual testing of component] | |||
===Global Navigation=== | ===Global Navigation=== | ||
Latest revision as of 20:14, 28 June 2024
(Group deadline: 21:00 28 June)
Introduction
This report presents a general design and detailed implementation of Hero, the resturant delivery robot. The goal of the design is to enhale Hero to autonomously deliver orders to specified tables while navigating a dynamic environment with obstacles and interacting with customers and staff of the resturant.
High-Level System Description
The primary task assigned to Hero is to deliver orders to specified tables within a restaurant environment. To accomplish this task, the system should contain several modules, each responsible for different aspects of the robot's functionality.
- Perception: This module processes laser data to detect obstacles in the environment.
- Localization: Responsible for tracking the robot's position as it moves.
- Global Navigation: Plans the path from the starting point to the target tables.
- Local Navigation: Handles short-range movements and obstacle avoidance.
- Don’t Crash: Ensures the robot stops before any collision.
- Interaction: Provides signals upon arrival at each table.
From Desires to Specs
The transformation of stakeholder desires into detailed specifications ensures Hero meets both technical and practical needs. The key stakeholder, the restaurant owner, seeks a reliable, efficient delivery robot that navigates safely, delivers orders on time, and interacts well with humans.
Environment Requirements
- Safety:
- No Damage: Hero should navigate without damaging the surroundings or itself.
- Obstacle Avoidance: Equipped with sensors to detect and avoid obstacles.
- Efficiency:
- Timely Delivery: Deal with stuck somewhere which will lengthen delivery time.
- Human Interaction:
- Signals: Provides clear signals upon arrival at tables.
Border Requirements
To achieve these environment requirements, the following border requirements should be taken into account:
- Collision Avoidance:
- Stop Mechanism: Stops immediately before potential collisions.
- Obstacle Detection: Mechanisms for detecting and rerouting when meeting obstacles.
- Handling Doors:
- Interaction with Humans: Capable of interacting effectively with humans, including handling doors if necessary.
System Requirements
These border requirements translate into specific system requirements as follows:
- Safety Margin:
- Breaking Distance: Defined to ensure safe stopping.
- Safety Features: Includes sensors and algorithms for real-time obstacle avoidance.
- Performance Metrics:
- Max Velocity and Acceleration: Defined to balance speed and safety.
- Mass: Considered in design to ensure stability and safety.
- Interaction Capabilities:
- Signal System: To indicate arrival and interact with human effectively.
By translating the desires into precise specifications, Hero is designed to operate efficiently and safely in a restaurant environment, meeting the needs of application.
System Architecture
Based on the system description, this section explained the system architecture design to enable the robot to perform the required tasks efficiently. Provide an overview of how components are integrated and interact with the state flow and data flow.
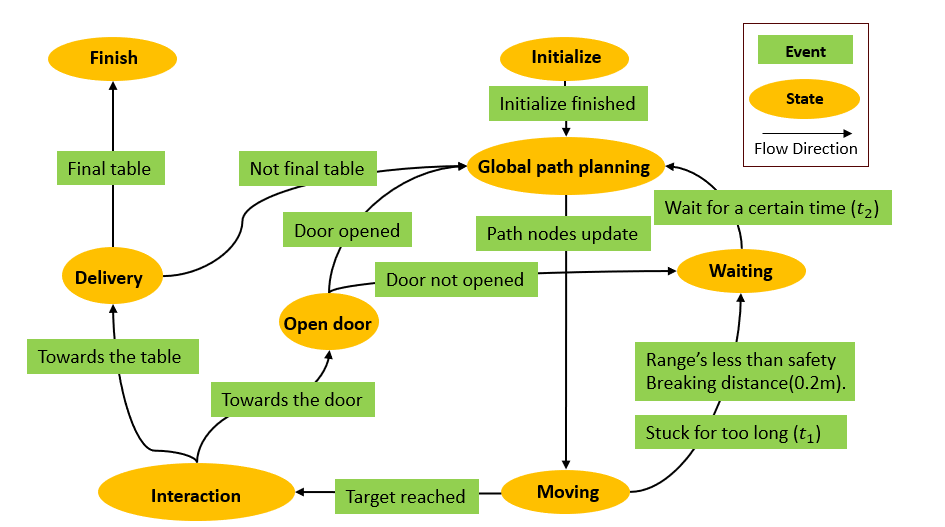
State Flow
The diagram illustrates the state flow of the designed system for the final challenge. To integrate all components, we utilized a state machine to manage the robot’s action in different scenarios. This approach provides a clear and organized framework for the combination of different functions. Thus, debugging is simplified, and the system's scalability is enhanced, allowing us to easily modify the states and transitions as needed. The specific state functions are described in detail in the following Component parts of the wiki page. The component names do not necessarily correspond strictly to the states.
The robot starts at the Initialize state. It begins with the localization process to determine the accurate initial position of the robot in the provided restaurant environment. Once it successfully gets the robot's location on the map, an initialization flag is set to true, and the robot proceeds to the Global path planning state. In this state, calculate an optimal path through the target table and update a list of target path nodes to the local navigator. Then, the robot forwards to the Moving state to begin navigation.
During the Moving state, the robot navigates toward its current target point through the dynamic window approach, using laser data and localization information to adjust its path and avoid obstacles. If the robot encounters a situation where it remains stuck for too long or too close to an obstacle, it transitions to the Waiting state. In this state, the robot waits s for a certain period of time to reassess the situation. If the robot remains stuck or encounters obstacles, it returns to the Global navigation state to generate a new path to the destination.
If the robot successfully reaches its target point, it moves to the Interaction state to confirm which target has been reached and adjust its position correspondingly. If the target is identified as the door, it moves to the Open door state and requests the door to be opened. The robot then monitors the door’s status. If the door is opened as requested, the robot returns to the Global navigation state to process a path through the door. If is not opened, the robot transitions to the Waiting state and repeats the situation reassess process.
If the target is identified as a table, the robot then adjusts its rotation toward the table and transitions to the Delivery state. In this state, the robot waits beside the table for the delivery task and uses the speaker modules of the robot to announce its current table number. Once the final table is reached, the robot transitions to the Finish state, indicating that all the delivery tasks are completed successfully.
In this process, designing different states and transition events ensures a systematic and reliable approach to robot navigation and task execution.
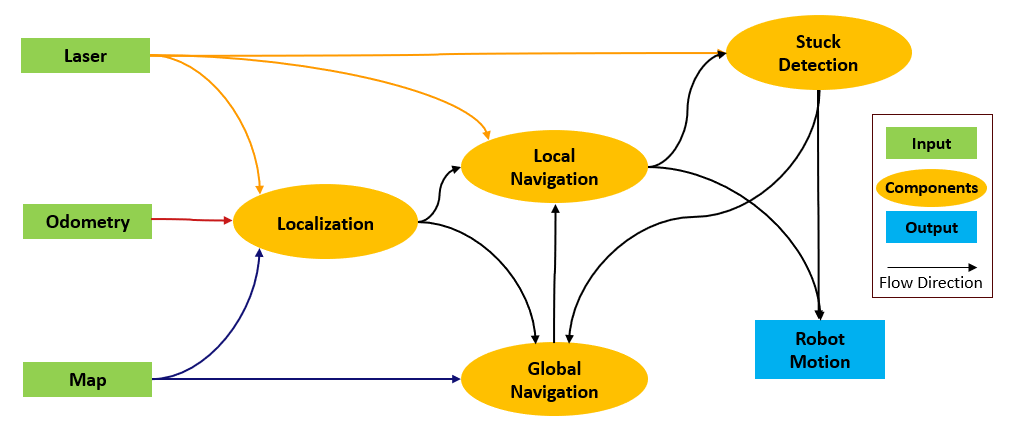
Data Flow
The data flow diagram illustrates the interactions between input sources, processing modules, and output commands for the robots. There are three major input sources: the laser and odometry come from the robot sensors, and the map is uploaded by the user. The map provides the existing representation of the restaurant environment, including the table positions and order information. The laser detects obstacles in the environment. The odometry supplies information regarding the robot’s position and velocity.
The Localization module first receives the data from all three inputs to determine the robot's position relative to the map. Over time, the robot's theoretical and actual positions will eventually diverge because of accumulated errors from odometry conversions between theoretical and real movement. Therefore, it’s fundamental to ensure that the robot knows its exact position within the environment during its movement for accurate navigation. The position is then forward to both Global Navigation and Local Navigation modules.
Global Navigation uses the map to plan an optimal path from the robot’s current position to the destination through the combination of PRM and A* algorithms and updates the current target point for Local Navigation. Local Navigation uses the current position, the target point, and the laser data to adjust the robot's path dynamically, avoiding obstacles and navigating through tight spaces. It provides control commands for linear and angle velocity to guide the robot's motion.
The Stuck Detection module handles abnormal status during the local navigation. If the robot is within 0.2 meters of an obstacle according to laser data or cannot find a path to reach its target points due to an unknown static obstacle or being stuck in a local minimum, the stuck detection module is triggered. It stopped the robot and initiated a path re-planning through the Global Navigation module.
The process involves a continuous feedback loop, constantly monitoring and adjusting the robot's movements based on inputs and environments to ensure safe and efficient navigation towards its destination.
System components
Initialization
Hero will start in the start area, defined by a rectangle of approximately 1 by 1 meters. The orientation of Hero is arbitrary.
In order to initialize the robot and obtain the current position of the robot for global path planning to complete the next tasks, the robot should move in the start area to obtain its positional information.
In the start area, the robot calls the functions in the localization function and moves and rotates in the region but does not go beyond the start area.
Localization
Localization is a critical component in the final challenge to ensure accuracy of actual position in the map during navigation. Given the random initial pose and accumulating error over time when solely using odometry data to calculate the pose, the localization module corrects the robot's position using sensor data and a map of the environment.
In localization module, particle filter algorithm is utilized based on the following procedure: A set of particles is initialized across the map, each representing a possible position of the robot. Each particle is assigned an initial weight and uniformly distributed. As the robot moves, each particle’s position is updated based on odometry data, which includes some randomness to account for motion noise. Then, it uses sensor data to perform measurement update, each particle’s weight is updated based on how well the data matches the expected laser data from that particle’s position. Particles have better match gets higher weights. Multinomial Resampling method is used to resample a new set of particles by drawing with replacement from the current set of particles, with the probability of drawing a particle proportional to its weight. This step helps focus the particles around the more probable positions and discards particles with low weights. Finally, the robot’s estimated position is determined by the weighted average or the most likely particle position based on the current set of particles.
We have tested the localization component individually in physical setup and the map is identical with the final challenge map. Firstly, a initial position was given to the Hero robot within specified region according to final challenge requirements. The tests involved starting from different initial pose and the result indicates that the particle converges quickly and the map inferred from estimated position align well with the actual final challenge map. The video tape of the individual test are shown in the link below. individual testing of component
For global path planning, A star and Probabilistic roadmap(PRM) are utilized. PRM generates vertices and edges to create a feasible map. This map is the input into the A star planner, which produces a node list and connections, thus providing a path between two specified points for global navigation.
Probabilistic Roadmap
The PRM works by randomly generating nodes in free spaces and then connecting these nodes with edges, based on the map with wall inflated. Nodes are randomly generated within the map, ensuring they are placed in free spaces not occupied by obstacles. The number of nodes is tuned to balance between computational efficiency and the complexity of the environment. Nodes are connected by edges, creates a network of possible paths that the robot can follow. By adjusting the number of nodes and connection distance , the PRM can be fine-tuned to find the most efficient paths in the restaurant environment.
A* search algorithm
The A* algorithm we implemented has two working modes: it can build a planner by obtaining connected nodes from the grid information or the PRM algorithm. Since the grid information of the map is not given in the final challenge, we use the sampling nodes and connections between nodes given by the PRM algorithm.
The idea of building a path planner based on PRM is as follows:
1. Read the coordinates of the start and end points from the configuration file. If the configuration file contains start and goal parts, overwrite the default values.
2. Get the number of nodes and connections in PRM and create a new node list and connection relationship container. Copy the node and connection information in PRM to the new node list and connection relationship container. Node ID starts from 2, and 0 and 1 will be used for the start and end points.
3. Create the start and end nodes and add them to the node list. Check the validity of the connection between the start and end points and the existing nodes, and establish a connection relationship.
4. Planner creation and initialization, set the initial cost [math]\displaystyle{ g }[/math] of each node to infinity, the heuristic cost [math]\displaystyle{ h }[/math] to the Euclidean distance from the node to the goal node, and the total cost to [math]\displaystyle{ g + h }[/math]. Create an open list to store the nodes to be processed, initially including the start node. Create another closed list to store the processed nodes.
5. Start path planning and select the node with the smallest total cost value in the open list for expansion. If the node is the target node, the path is found and the loop ends. Otherwise, add the neighbor nodes of the current node to the open list and update their initial cost value, total cost value and parent node. Remove the current node from the open list and add it to the closed list.
6. Starting from the target node, trace back to the parent node and generate a path.
7. The return value of the planner contains the node list, connection relationship, start and end nodes.In the main program, the A* algorithm is called before the while loop and after the PRM call. By adding reasonable conditional judgments and printing content, we ensure that the nodes and connection content can be read from the generated PRM image results. In order to deal with the situation where the node connection generated by a certain call to the PRM algorithm is unreasonable due to improper PRM parameters and the randomness of PRM, and then A* has no solution output, we set the corresponding judgment conditions. In this case, PRM and A* are called again. Ensure that there is an executable node list in the final pass to the local navigator.
Dynamic Window Approach
Given a target point by global navigation algorithm and positions of obstacle by laser sensor, local navigation aims to calculate an available path to avoid collision with the obstacles as well as to move towards the target point. The outputs of all local navigation algorithms shown in lectures are directly the desired velocities [math]\displaystyle{ (v, \omega) }[/math] ([math]\displaystyle{ v }[/math] is linear and [math]\displaystyle{ \omega }[/math] is angular velocity) of the robot. There is no need to perform a path following task.
In exercising, we implemented both Artificial Potential Filed (APF) Algorithm and Dynamic Window Approach (DWA). At first, we chose APF as our local navigation algorithm because of its robustness and simplicity. However, during the test we found that APF is not ideal for vertex handling and the robot will oscillate when driving through a corridor, whereas DWA can generate smoother trajectories and shows great potential for dealing with complex scenarios. And DWA is designed to deal with the constraints imposed by limited velocities and accelerations, because it is derived from the motion dynamics of the mobile robot. This is well suited to the realities of Hero. Moreover, DWA contains the idea of optimal control, which can improve the efficiency of the robot. Thus, we switched to DWA.
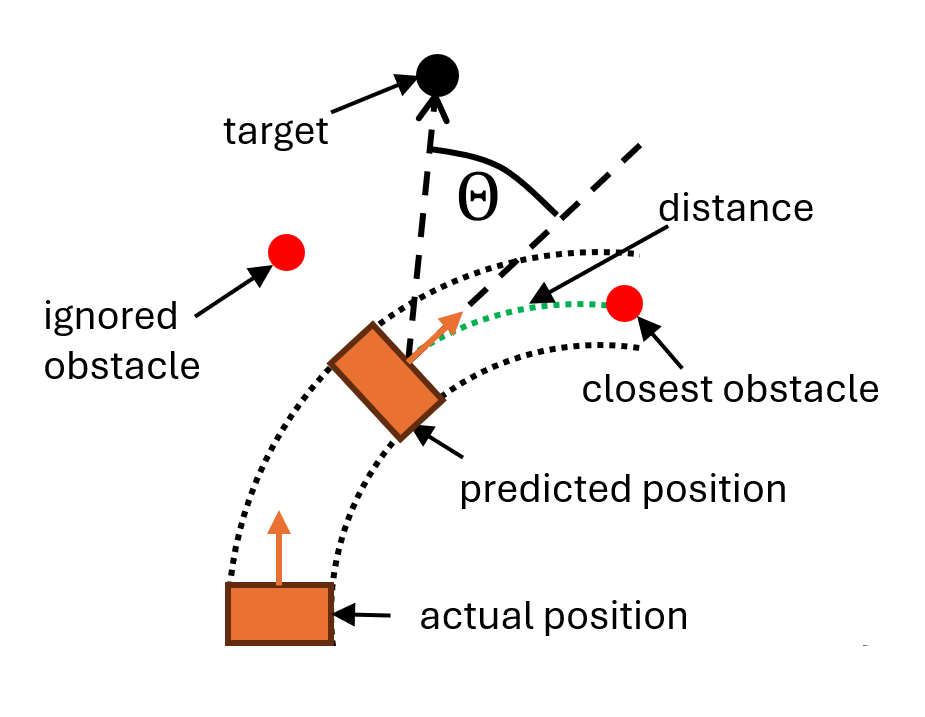
DWA performs reactive collision avoidance. When computing the next moving command, DWA considers only a short time interval, within which the robot's velocities [math]\displaystyle{ (v, \omega) }[/math] are considered to be constants. The algorithm will evaluate the results of all possible velocities and select the optimal one. Instead of using the simplified version introduced in lectures, we use the original version of this algorithm proposed by D. Fox, etc.[1] The main difference is that the original algorithm uses a more refined geometric model when calculating the distance between the obstacle and the predicted trajectory, taking both the trajectory and the robot size into account. As shown in figure on the right, the obstacles that are not on the trajectory will be ignored. And by including a safety margin, we can control the minimum distance between obstacles and Hero.
The set of all possible velocities [math]\displaystyle{ V_r }[/math] is called the search space. It is the intersection of three sets: [math]\displaystyle{ V_r = V_s\cap V_a\cap V_d }[/math], where [math]\displaystyle{ V_s }[/math] is the set of velocities that are limited by robot's dynamics, [math]\displaystyle{ V_a }[/math] is the set of velocities with which the robot can stop before reaching the closest obstacle and [math]\displaystyle{ V_d }[/math] is the set of velocities constrained by current velocities and acceleration.
These three sets are defined as:
[math]\displaystyle{ \begin{align} \begin{matrix} V_s =&\left\{v,\omega |v\in[v_{min},v_{max}]\wedge \omega\in[\omega_{min},\omega_{max}] \right\}\\ V_a =&\left \{v,\omega |v\le \sqrt{2d(v,\omega )\dot{v}_b } \wedge \omega \le \sqrt{2d(v,\omega )\dot{\omega }_b} \right \}\\ V_d =&\left \{v,\omega |v\in [v_{a}-\dot{v}\Delta t,v_{a}+\dot{v}\Delta t] \wedge \omega \in [\omega_{a}-\dot{\omega}\Delta t,\omega_{a}+\dot{\omega}\Delta t] \right \} \end{matrix} \end{align} }[/math]
where [math]\displaystyle{ \dot{v}_b }[/math] and [math]\displaystyle{ \dot{\omega }_b }[/math] are maximum deceleration values and [math]\displaystyle{ d(v,\omega) }[/math] is the distance to the closest object; [math]\displaystyle{ v_a }[/math] and [math]\displaystyle{ \omega_a }[/math] are actual velocities and [math]\displaystyle{ \dot{v} }[/math] and [math]\displaystyle{ \dot{\omega} }[/math] are maximum acceleration values.
[math]\displaystyle{ V_s }[/math] and [math]\displaystyle{ V_d }[/math] ensure that the selected reference velocities is consistent with the physical limitations of the robot. And [math]\displaystyle{ V_a }[/math] ensures that the robot does not collide, because the distance item of velocities that lead to collision will be zero, making these velocities unavailable.
Implementation in C++
As shown in the figure on the right, the DWA is basically a discrete search to maximize the reward function. Considering the large number of parameters of DWA, we implement DWA as a class in C++ and make those parameters as class-scope private constants. There are two advantages to such an implementation.
Firstly, with the limitation of class scope and constant private variables, these parameters will not be accessible to other code, which guarantees these parameters will not be modified by other code and helps to improve code clarity.
Secondly, packaging all the parameters of DWA in a single class helps to improve the portability of the code. One can easily use this code by including a head file. And if we want to change these parameters only, we can simply re-compiler this part solely and then link it with others, instead of re-building the whole project. The reason we didn't use a file (such as JSON or XML) to configure these parameters is that we want the compiler to perform compile-time constants optimization, as these parameters should be known constants in the final challenge.
Parameter Tuning and Test
We tune the parameters in three steps:
- We did some experiments to obtain parameters determined by the physical constraints of the robot, such as the size of the robot, the minimum safe stopping distance and the maximum velocities of the robot.
- Then we tune the weight of heading item and distance item in DWA reward function, to make a trade-off between avoiding obstacles and moving towards the target point.
- Increase the weight of the velocity item to ensure that the robot tends to choose a faster speed rather than rotating in place.
To test in simulation, we wrote some publishers to publish the predicted trajectories. The Code can be found in "DWA_publisher" branch in GitLab repository. There are three publishers publishing three topics: "predicted_path", "crash_path" and "selected_path".
- "predicted_path" consists of all available trajectories produced by velocities in [math]\displaystyle{ V_r }[/math];
- "crash_path" contains all trajectories in [math]\displaystyle{ V_s }[/math] and [math]\displaystyle{ V_d }[/math] but not in [math]\displaystyle{ V_a }[/math].
- "selected_path" is the optimal path selected by DWA.
With these topics, we can visualize all trajectories in "rviz" by modifying its configuration. The result is shown in Simulation_test.mp4. The green lines are trajectories in topic “predicted_path”, and blue lines are trajectories in topic "crash_path". The red one is the trajectory of topic "selected_path". It can be observed that the DWA can perform the obstacle avoidance task well, choosing a trajectory among the many available paths that maintains a safe distance from the obstacles and keeps approaching the target point.
After combining DWA with global navigation, we tested it on Hero. After tweaking the parameters for further customization and fixing some minor bugs, DWA worked well as expected. As you can see in the video of the final challenge, the robot successfully avoided the chairs in front of the table and the people moving around. It should be noted, however, that even if we optimize the parameters as much as possible, the robot can still get trapped in local optimal solutions. Eventually we decided to solve this problem through a state machine. See the section on state flow for more details.
Interaction
When the robot reaches the target table location, it turns to the direction of the table and performs voice interaction. This function is realized as follows.
1.Checking if the Robot is Near the Table
We first checks if the robot is within a specified proximity to a target location. It uses a boolean flag to ensure the task is performed only once. By calculating the distance between the robot's current position and the target position, the system can determine if the robot is close enough to proceed with the next steps.
2.Updating the Flag and Outputting Information
Once the proximity condition is met, the system updates a flag to prevent redundant execution of the same task. It also logs the current state for debugging purposes, providing feedback on the internal status of the task completion.
3.Calculating the Target Angle
The principle for calculating the angle the robot needs to rotate is as follows: First, calculate the direction angle towards the target table by using the difference between the target table's position and the robot's current position (using the atan2 function). Then, determine the angle the robot needs to rotate by calculating the difference between the robot's current orientation and the target direction angle.
4.Rotating the Robot
The system uses a loop to adjust the robot's orientation incrementally until the desired angle is reached. Within this loop, it continuously sends rotation commands and updates the robot's pose with new sensor data. This iterative approach ensures precise alignment with the target direction.
5.Stopping the Rotation and Reporting Arrival
Once the robot reaches the target angle, the code outputs a message indicating that the robot has arrived at the table. It sends a command to stop the robot's rotation and makes the robot speak to report that it has arrived at the table.
When the robot reaches the door, the robot presents a voice prompt requesting the door to be opened and when the robot checks that the door has been opened, the robot passes through the door. This function will be realized in the following steps
1.Detecting Door Presence and Status
The design includes a mechanism to determine whether doors are open or closed. This is achieved using sensors such as cameras or LIDAR to scan the environment. When the robot detects a door within the specified range (0.5-1m width), it assesses whether the door is open or closed using sensor data analysis.
2.Positioning in Front of the Door
Once a door is detected and identified as closed, the system navigates the robot to position itself directly in front of the door. This involves calculating the optimal path to the door and moving the robot to the desired location, ensuring it is correctly aligned with the door.
3.Requesting the Door to be Opened
When the robot is in position in front of a closed door, it utilizes its speech interface to request that the door be opened. This involves generating a vocal command that asks for assistance in opening the door.
4.Verifying the Door is Open
After requesting the door to be opened, the system continuously monitors the door's status to verify whether it has been opened. This is done by repeatedly checking the sensor data to detect any changes in the door's state. The robot waits in front of the door until it confirms that the door is open.
5.Proceeding Through the Door
Once the door is verified to be open, the system navigates the robot through the doorway to continue its task.
Final Challenge Results
Results Analysis
Until the final challenge, we did not successfully integrate the localization code, so we used the backup code in the final challenge. The code only includes the local navigator of DWA and the global navigator using PRM and A*. And added the following functions: update the robot position information according to the Odometry data, determine whether it has reached the table position based on the position information, turn on the spot after reaching the table, make the robot face the table, and give a clear arrival prompt. Then return to the original direction and use the local navigator to go to the next table. Repeat the above steps for any table until you reach the end of the node list given by the global navigation.
In the first round of robot testing, we did not successfully reach the first table because the actual starting position of the robot did not match the map position specified in the config file. The actual position was to the left of the ideal specified position, which caused the first table to cross the robot's global navigation trajectory. It encountered obstacle avoidance behavior generated by local navigation at the first table, which also prevented it from getting close to the table position we specified to determine the location. The judgment condition for the table position is a one-time flag and a real-time calculation of the Euclidean distance between the current position and the specified table position. Therefore, the wrong robot starting position made the subsequent path and table position judgment invalid. The robot always believed that it had not reached one of the node lists, so it tried to return by turning at a large angle and reach the coordinate position corresponding to that node. However, since the node coordinates are in the actual table position, the robot cannot reach them, so the first attempt was not successful. The video can be checked in
In the second attempt, we adjusted the robot's starting position and gave instructions to control movement during normal program operation, but the robot did not move. We were later told by the TA that this was due to an unknown robot hardware failure. Therefore, we were given a third attempt.
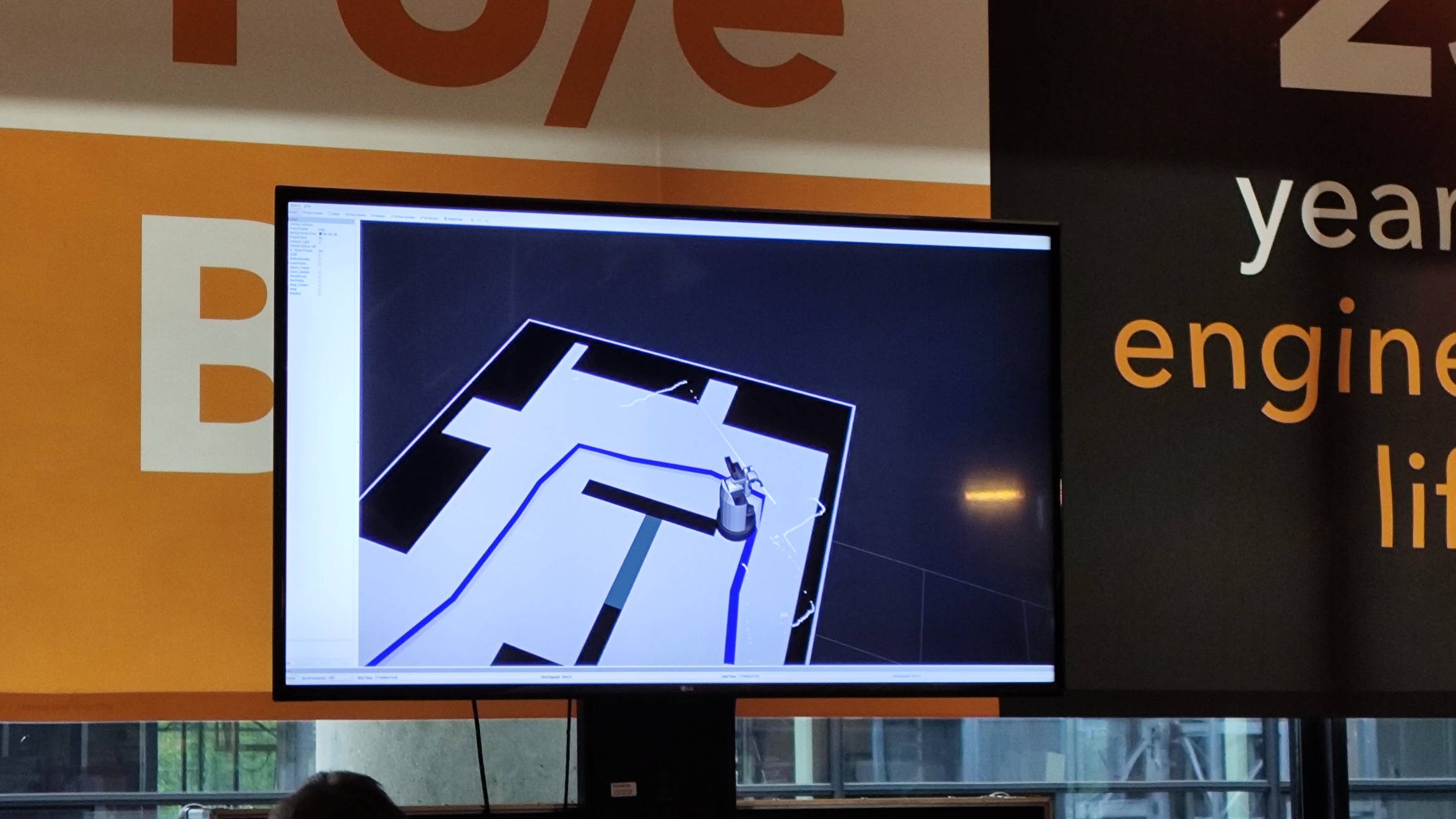
In the third attempt, after rigorous distance measurement, we used the relatively correct actual robot starting coordinate position. After calling PRM and A* global navigation, the robot generated a node list and provided it to the DWA algorithm to perform local navigation, track each node and refresh the node according to the list. After a period of straight tracking, we arrived near Table 0. When the Euclidean distance condition and the one-time flag judgment condition were both met, the "reaching the table" program was entered. The robot stopped on the spot and rotated 90 degrees to the left on the spot to make the robot face the dining table. The robot gave an obvious arrival prompt sentence "I arrived at table zero", then stopped for 5 seconds, rotated 90 degrees to the right on the spot, and the program returned to the normal tracking state. The robot went to Table 1. In the final challenge, it was not necessary to reach Table 1, so we blocked the flag for Table 1 and would not enter the execution state of Table 1. There is also a chair as an obstacle in the vicinity of Table1. The obstacle partially passes through the node coordinates generated by global navigation. Here, the DWA algorithm takes effect and helps the robot avoid the chair. After passing Table 1 and crossing the obstacle, the robot continues to move toward Table 2, and the arrival state for Table 2 is also triggered near Table 2. The arrival state content of Table 2 is as described in Table 0 above. When the robot returns to the normal tracking state after executing Table2, we find that the robot's return rotation angle does not match the robot's rotation angle to face Table 2. This is because the ground is slippery and the odometry method has errors in the cumulative calculation of angles. As the robot travels more distance, the odometry self-addition calculation method will inevitably have errors in coordinate information and angle information, and the errors will gradually increase. We did not use the localozation method, so this problem is inevitable. This results in the robot thinking that its position and orientation do not match the actual position and orientation of the robot, and we have no ability to correct this error. In the visual interface, we can clearly notice that the laser data's detection of the surrounding walls no longer matches the shape characteristics of the surrounding walls in the map interface, with a deviation of more than 45 degrees, as the picture "Final_chellenge_odomety_error.jpg" shows on right. This error causes the robot to think that the coordinate information of the nodes on the path appears in the wall, which cannot be solved by local navigation or global navigation. The robot cannot reach the coordinates of the next node, resulting in the node being unable to update, and finally the robot does not reach Table 4. Only after reaching Table 4 will it enter the state of looking for Table 3 and "requesting to open the door." Therefore, the subsequent states cannot be achieved. The third attempt video can be checked in https://youtu.be/rsaSeHmI8x0?si=TT72kvpm_uKB_8LR
The summary of the Final Challenge is as follows:
1. The robot needs to set an accurate actual starting position, which strictly complies with the coordinate information and orientation information provided by the config file. This can be ensured by manual measurement of the actual map. If the robot's starting position deviates, it will cause the map information and global navigation trajectory information to deviate, which will affect the deviation of the robot's actual map motion trajectory.
2. Since localization is not used, a carefully designed config file and initial and final coordinate information must be provided to the robot for global navigation. The robot coordinates and orientation information must be calculated using the self-addition method of odometry.
3. Odometry calculations will continue to accumulate coordinate information errors, which will increase as the robot travels farther. This phenomenon will be exacerbated if the robot is running on a slippery surface or making frequent turns. This will eventually lead to unreliable coordinate information. We didn't see this error in simulation but it is vital for real robot test.
4. The Table judgment condition we provide for the robot relies heavily on the Euclidean distance calculation between a specified coordinate position and the current robot position. If the robot's current position is wrong, the robot cannot correctly enter the state of reaching the Table.
Future Improvement
It's a pity that we didn't manage to accomplish all our goals in the final challenge. Here we list the parts that can be further improved in the future.
Localization
We actually have finished the localization algorithm solely. However we failed to combine with navigation algorithm. In the final challenge, we rely on odometry data to obtain the location of the robot instead of using localization algorithm. It is therefore essential that the initial position of our robot is accurate and known, as even small errors can cause the global navigation algorithm to drift. And as the robot continued to move on the smooth floor, the cumulative error caused the robot to eventually lose its positional information. By involving the Localization algorithm, the robot can continuously locate itself through laser data, thus avoiding the problems mentioned above.
The introduced DWA algorithm only considers the angle between the robot and the target point. It tries to force the robot move towards the target point by increasing the velocity weights, however, this indirect implementation detracts from the intuitive nature of the parameter tuning process. It is easy for the robot to wander locally instead of going to the goal point. Therefore, we would like to introduce a penalty in the reward function for the Euclidean distance of the robot from the goal point, thus forcing the robot to move towards the goal point more directly. Moreover, the reward function used by the algorithm is a conjugate form of linear programming. There might be multiple optimal solution. If the computational complexity is durable, it would be better to transfer it to a convex quadratic programming which only have one global optimal solution.
Open door
As required and as happened in the final challenge, there are situations where the known paths are completely blocked, at which point the robot needs to pass through a door that may be closed. As the designed in state flow, the robot should be able to stop in front of a door to detect if the door is open. This can be done by a small modification in global navigation, i.e. If the path generated by the global algorithm passes through the door, the global algorithm should terminate, setting a point in front of the door as the final goal point. This allows the robot to travel to the front of the door and then detect if the door is open.
State flow
Before the final challenge began, we had completed the overall design of the state machine but failed to implement the code integration. The exception handling mechanism designed in the state machine did not work properly, making our robot very vulnerable to disturbances and unexpected situations. For example, if the robot gets stuck in a local optimal solution or the current path is not feasible, our robot will not be able to re-invoke the global navigation algorithm to regenerate a reference path.
Reference
- ↑ D. Fox, W. Burgard and S. Thrun, "The dynamic window approach to collision avoidance," in IEEE Robotics & Automation Magazine, vol. 4, no. 1, pp. 23-33, March 1997, doi: 10.1109/100.580977. keywords: {Collision avoidance;Mobile robots;Robot sensing systems;Orbital robotics;Robotics and automation;Motion control;Humans;Robot control;Motion planning;Acceleration},