Mobile Robot Control 2024 R2-D2: Difference between revisions
Tag: 2017 source edit |
|||
| (17 intermediate revisions by the same user not shown) | |||
| Line 496: | Line 496: | ||
= Final Challenge : Hero, the new age waiter = | = Final Challenge : Hero, the new age waiter = | ||
== | == Videos of the final challenge == | ||
* | * The video of the designed system running on the real robot during the final challenge on 21 June 2024: https://youtu.be/ncUWcO743BM (3rd attempt) | ||
* | * The video of initial attempts for the designed system for final challenge: https://youtu.be/-lya73TgR88 (1st and 2nd attempt) | ||
* Simulation Testing video on the final challenge RestaurantMap2024: https://youtu.be/VLNTw9IdH2I | |||
* | * Simulation Testing video on the final challenge RestaurantMap2024 with Variations and Moving Obstacles: https://youtu.be/_71ev8N3lXI | ||
* | |||
https://youtu.be/ | |||
== Introduction == | == Introduction == | ||
| Line 595: | Line 588: | ||
If an occupied spot is encountered, it calls the replanning module which generates an alternative path for docking around the table. | If an occupied spot is encountered, it calls the replanning module which generates an alternative path for docking around the table. | ||
=== Global Navigation | === Global Navigation === | ||
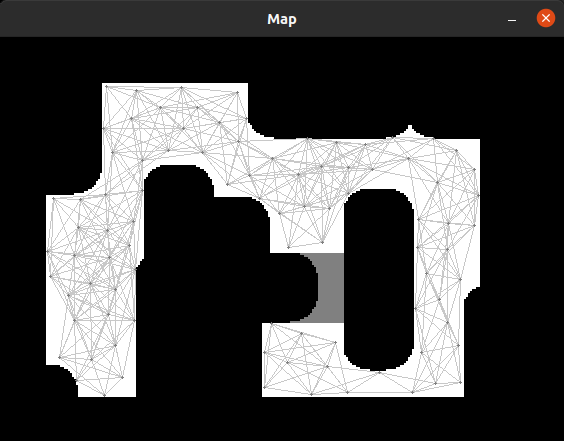
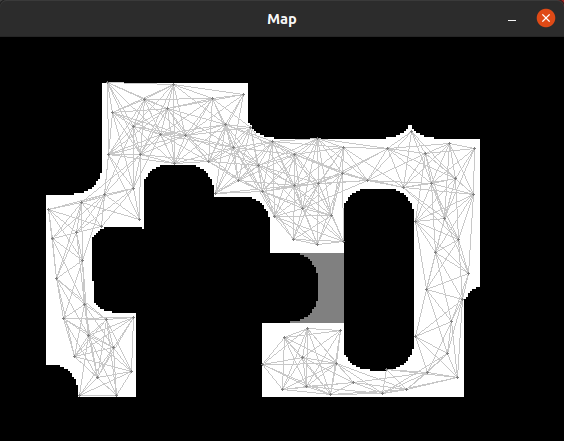
For global planning, the PRM (Probabilistic Roadmap) code from the project was utilized. Due to the requirement to visit each table sequentially, a single PRM planning is conducted for global planning, and the A* algorithm is employed for path planning each time a table is visited. Based on the simulated map data, the resolution of PRM is set to 0.025 pixels. To ensure that nodes are not generated between two tables (since the robot's width cannot fit between tables, making those nodes unreachable), the wall expansion coefficient is set to 0.58, thus preventing the generation of nodes too close to any surface. Additionally, we need to adjust the grayscale recognition to ensure that gray doors are not identified as walls, thereby allowing paths that pass through doors to be generated. | [[File:Final map nodes.png|thumb|Final Challenge Map Global Planning Nodes]] | ||
For global planning, the PRM (Probabilistic Roadmap) code from the project was utilized. Due to the requirement to visit each table sequentially, a single PRM planning is conducted for global planning, and the A* algorithm is employed for path planning each time a table is visited. Based on the simulated map data, the resolution of PRM is set to 0.025 pixels. To ensure that nodes are not generated between two tables (since the robot's width cannot fit between tables, making those nodes unreachable), the wall expansion coefficient is set to 0.58, thus preventing the generation of nodes too close to any surface. Additionally, we need to adjust the grayscale recognition to ensure that gray doors are not identified as walls, thereby allowing paths that pass through doors to be generated.To enhance the stability of the PRM algorithm, additional algorithms were incorporated to increase the number of nodes generated around tables. This ensures that even if one or several nodes are occupied, alternative nodes can still serve as endpoints near the tables. | |||
To enhance the stability of the PRM algorithm, additional algorithms were incorporated to increase the number of nodes generated around tables. This ensures that even if one or several nodes are occupied, alternative nodes can still serve as endpoints near the tables | |||
To ensure that the robot can be controlled to visit tables in a specified order by inputting table numbers, the coordinates of the four corners of each table are stored in a configuration file. An algorithm matches the table numbers to their respective coordinates, ensuring that the table coordinates can be directly recognized. In the goal selection algorithm, the input number is first mapped to the corresponding table coordinates. Then, the algorithm searches for PRM-generated nodes near the table and selects the node closest to the current starting point as the target point. | To ensure that the robot can be controlled to visit tables in a specified order by inputting table numbers, the coordinates of the four corners of each table are stored in a configuration file. An algorithm matches the table numbers to their respective coordinates, ensuring that the table coordinates can be directly recognized. In the goal selection algorithm, the input number is first mapped to the corresponding table coordinates. Then, the algorithm searches for PRM-generated nodes near the table and selects the node closest to the current starting point as the target point as mentioned in path planning state. | ||
In practical operation, the robot initializes and confirms its current coordinates. | In practical operation, the robot first initializes and confirms its current coordinates. After the path is generated and the final goal that is the first table is reached, the robot re-plans the path using its current coordinates as the new starting point and the next goal as the endpoint. This process continues iteratively until the robot reaches the final goal. This approach allows for the dynamic switching of goals and robust path planning by incorporating Localization, thereby avoiding errors that could arise from using the previous endpoint's coordinates as the new starting point. | ||
=== Replanning | === Replanning === | ||
In path replanning, we need to consider two scenarios. The first scenario occurs when there is an obstacle on the current path. According to DWA settings, if the next node is occupied by an obstacle, the robot will stop until the node becomes available. To avoid this situation, it is necessary to replan a path around the obstacle while maintaining the same goal. The second scenario arises when the goal is occupied or there is an obstacle nearby, preventing access to the intended goal. In this case, a new goal must be selected to conclude the current path planning. | In path replanning, we need to consider two scenarios. The first scenario occurs when there is an obstacle on the current path. According to DWA settings, if the next node is occupied by an obstacle, the robot will stop until the node becomes available. But if it does not move, the robot will stay there indefinitely. To avoid this situation, it is necessary to replan a path around the obstacle while maintaining the same goal. The second scenario arises when the goal node neat the table is occupied or there is an obstacle nearby, preventing access to the intended goal. In this case, a new goal must be selected to conclude the current path planning. | ||
[[File:Blocked path.png|thumb|The region near the starting point was marked blocked by the robot as inaccessible due to presence of an unseen static object.]] | |||
To determine the need for replanning, we integrate data from the laser sensor. When the laser sensor detects an obstacle ahead that impedes movement, we read the sensor data to calculate the obstacle's width. By combining the obstacle's width with the global planning node information, we assess whether the obstacle obstructs subsequent paths. If the subsequent nodes are deemed inaccessible, path replanning is initiated; otherwise, the obstacle is simply bypassed. Additionally, we monitor the robot's speed. If the robot's speed is zero for more than 10 seconds, the system will trigger replanning. For scenarios where the goal node is inaccessible, the laser sensor detects if the goal node is occupied and compares the robot's current coordinates with the goal coordinates. If the sensor data indicates that the current distance to the node is greater than the distance to the obstacle, the goal replanning process is initiated. | |||
During path replanning, the first step involves measuring the obstacle's width using the laser sensor and constructing a rectangle in the PRM map with a side length equal to the measured width. The starting edge of the rectangle is the distance detected from the obstacle. Using the robot's current coordinates and the distance measured by the laser sensor as references, we calculate the approximate position coordinates of the obstacle. Before running the PRM algorithm again, we update the simulated map to mark this area as an impassable region (displayed as a black area on the map). Then, the PRM algorithm is rerun to generate new paths and nodes, keeping the original goal node unchanged. Using the robot's current coordinates as the starting point, the A* algorithm is employed to replan the path. | |||
For goal replanning, the steps are similar. The only difference is that after confirming the goal is obstructed, the goal selection algorithm is rerun to choose an alternative accessible node. If the path to this node is not obstructed, the goal is updated to this new node, and the A* algorithm is rerun to plan the path. If the path remains impassable, other nodes are selected until a feasible path is found. If all nodes are obstructed, the obstacle is marked, and the PRM is rerun. | |||
The simulation video to display working of replanning can be found here: https://youtu.be/dWZ9Ip53ogI | |||
=== Localization === | === Localization === | ||
| Line 623: | Line 617: | ||
There are 5 tables in the map, in each circle we set a table as the destination of global planning. According to the given svg map, we manually set the center point of each table, as shown below. | There are 5 tables in the map, in each circle we set a table as the destination of global planning. According to the given svg map, we manually set the center point of each table, as shown below. | ||
"tables": | |||
[[ 75, 320], [ 75, 190], [310, 290], [185, 50], [365, 50]]. | |||
When robot is planning to reach table, PRM will be used to generate nodes. | When robot is planning to reach table, PRM will be used to generate nodes. | ||
The code will go through all the nodes, only considering the nodes which stand in the rectangular(diagonal: current position, table centre), | The code will go through all the nodes, only considering the nodes which stand in the rectangular(diagonal: current position, table centre), | ||
| Line 641: | Line 635: | ||
[[File:NodeBetweenTables.png|alt=A node can be generated between table 1&2|thumb|A node can be generated between table 1&2]] | [[File:NodeBetweenTables.png|alt=A node can be generated between table 1&2|thumb|A node can be generated between table 1&2]] | ||
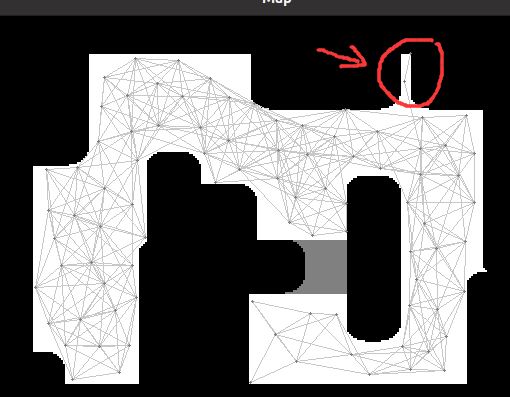
A failure scenario identified during testing was the lack of a clearly defined distance within which a robot is considered to be serving. Consequently, there is no specific limitation to control the distance between the goal node and the table center in the code. For instance, the code tends to select nodes located between tables 1 and 2 as the goal node (as shown in the red circle in the image, with an "infl_radius" of 0.58). However, this gap distance conflicts with the "dont_crash" code or "clearance_radius," causing the robot to stand still between the tables and fail to reach the goal node. Even if the robot reaches the goal node, it cannot move backward and needs a diameter to turn around. The narrow gap conflicts with the DWA algorithm, preventing the robot from exiting the gap. These problems can be resolved by increasing the inflation radius in the PRM, ensuring the gap between tables is filled, and no nodes are generated between the tables. However, increasing the inflation radius also increases the distance between the table and the robot's serving point. | A failure scenario identified during initial testing phase for final challenge was the lack of a clearly defined distance within which a robot is considered to be serving. Consequently, there is no specific limitation to control the distance between the goal node and the table center in the code. For instance, the code tends to select nodes located between tables 1 and 2 as the goal node (as shown in the red circle in the image, with an "infl_radius" of 0.58). However, this gap distance conflicts with the "dont_crash" code or "clearance_radius," causing the robot to stand still between the tables and fail to reach the goal node. Even if the robot reaches the goal node, it cannot move backward and needs a diameter to turn around. The narrow gap conflicts with the DWA algorithm, preventing the robot from exiting the gap. These problems can be resolved by increasing the inflation radius in the PRM, ensuring the gap between tables is filled, and no nodes are generated between the tables. However, increasing the inflation radius also increases the distance between the table and the robot's serving point. | ||
An improvement done was that we | An improvement done was that we choose the node closest to table edge instead of choosing the node closest to the table centre. In json file, tables are constructed by segments, and each segment of individual table is given by four points. | ||
"tables": | |||
[ [49, 50], [50, 41], [41, 40], [40, 49]], | |||
[[File:Distance from a point to a segment.png|thumb|Distance from a point to a segment<ref>Shortest distance between a point and a line segment https://i.sstatic.net/sXc2j.png</ref>]] | [[File:Distance from a point to a segment.png|thumb|Distance from a point to a segment<ref>Shortest distance between a point and a line segment https://i.sstatic.net/sXc2j.png</ref>]] | ||
For example, in the new goal selection algorithms, it will go through all nodes, and find the node which is closest to any segment of the table, and set that node to the goal node of serving table. | For example, in the new goal selection algorithms, it will go through all nodes, and find the node which is closest to any segment of the table, and set that node to the goal node of serving table. | ||
| Line 660: | Line 654: | ||
=== Opening the Door === | === Opening the Door === | ||
To implement the task of opening a door for the final challenge, the code first retrieves the robot's current position with coordinates x and y. It then checks if the robot is near the door by using the `isNearDoor` function, with a distance threshold of 0.5 units. If the robot is within this threshold, it stops the robot by sending a base reference of (0, 0, 0) to halt its movement. The code then pauses the robot's activity for five seconds using `std::this_thread::sleep_for`. After the pause, the robot announces "open the door" using the `io.speak` function. Following this, the robot resumes its tasks by calculating the next step of its Dynamic Window Approach (DWA) algorithm using `lp.dwa_step`, which considers the current position and point cloud data. Finally, the new velocity commands are sent to the robot's base to continue its movement. | |||
replanning through the door, | If the door does not open, the replanning will be triggered to find an alternative route towards the goal. Another thing to notice here is that, when the robot is trying to cross the door boundary, Localisation particles are seen to blow-up. This was a major problem because the robot is clueless when trying to pass through the door. Additionally, due to this, we can see that it takes a lot of time for the system to process this transition and eventually making the robot to move very very slowly through the door. This issue can also trigger unwanted replanning even if the door was opened and robot is passing safely through it. | ||
The simulation video can be found here: https://youtu.be/J_RSyXLSdz4 | |||
= Final Challenge Results = | = Final Challenge Results = | ||
Final Results Videos can be found in the starting of the final challenge report. | |||
== First Two Tries == | == First Two Tries == | ||
Revision as of 21:01, 28 June 2024
Introduction
This the wiki of the R2-D2 team for the course Mobile Robot Control of the Q4 in the year 2023-2024. The team is consisted from the following members.
Group members:
| Name | student ID |
|---|---|
| Yuri Copal | 1022432 |
| Yuhui Li | 1985337 |
| Wenyu Song | 1834665 |
| Aditya Ade | 1945580 |
| Isabelle Cecilia | 2011484 |
| Pavlos Theodosiadis | 2023857 |
Week 1 - The art of not crashing
This code periodically reads sensor data (laser and odometry) and adjusts the robot's movement in real-time based on this data. Specifically, when an obstacle is detected in front, the robot stops; otherwise, it continues to move forward. This control method uses a fixed-frequency loop and conditional checks to achieve simple obstacle avoidance.
Approximate flow of algorithm:
- Initialize Input/Output and Frequency Control Objects: Create objects to manage sensor data reading and control command sending, as well as an object to control the loop frequency.
- Enter the Main Loop: Keep the loop running until a certain condition (e.g., loss of connection) stops the loop.
- Read Sensor Data: In each loop iteration, read the necessary sensor data (e.g., laser data and odometry data).
- Evaluate Conditions and Send Control Commands:
- If the sensor data meets specific conditions (e.g., detecting an obstacle), send a stop command.
- Otherwise, send a forward or other appropriate control command.
- Control Loop Frequency: Ensure the loop runs at the preset frequency to maintain real-time control and stability.
This method can be applied to various robot control scenarios by periodically acquiring environmental perception data and adjusting the robot's behavior in real-time based on predefined logic, thus achieving the desired functionality.
Simulation
Pavlos
My idea was to use the LiDAR sensor to detect any objects directly on the front of the robot. Thus when the robot would move forward it would detect the distance from the object directly on the front of it and stop before reaching a predefined threshold. In the video the threshold was 0.5 meters. To detect the distance exactly on the front I used the measurement in the middle of the ranges list of a laser scan message. I also created a function which takes as an argument a laser scan message and an angle in degrees and returns the distance measurement of the ray at that angle.
Video displaying the run on the simulation environment:
https://www.youtube.com/watch?v=MXB-z1hzYxE
Isabelle
I took the laser reading at the middle angle by taking the middle value of the reading range, together with the two readings before and after it. The robot moves forward by default and if these values go under 0.3m, it will stop.
Video of the program in action: [link]
Wenyu
Video record of dont_crash implementation & measurements: https://youtu.be/brgnXSbE_CE
Aditya
For this assignment I decided to improve upon the existing code of my group member Pavlos. Because I had the similar idea on the implementation of dont_crash as him, I decided to make the robot do more than what was asked for using the existing implementation. I developed a function turnRobot and made a loop in main code that makes the robot turn 90 degrees in the left direction as soon as it detects an obstacle infront of it and continue to move forward until it detects another obstacle and the process is repeated again. It is observed that the robot does not make a perfect 90 degrees turn and also because of this, it crash in the wall at a slight angle. I think this is because the loop works for only one laser data reading that is measured directly from the front. To fix this, I can create a loop which takes a range of laser angles from the front and takes a turn depending on the angle at which it detects the obstacle.
The simulation video can be found here https://youtu.be/69iLlf4VPyo
Yuri
I immediately started with the Artificial Potential Field method as my "don't crash" implementation.
Yuhui
This code controls a robot's movement based on laser and odometry data at a fixed frequency (10Hz). When the laser or odometry data is updated, the robot moves forward at a speed of 0.1 meters per second. If any laser scan point detects an obstacle closer than 0.4 meters, the robot stops moving. The emc::IO object is used to initialize and manage input/output operations, while the emc::Rate object controls the loop's execution frequency. The functions io.readLaserData(scan) and io.readOdometryData(odom) read laser and odometry data, and the io.sendBaseReference function sends speed commands to control the robot's movement. Video of the program: https://youtu.be/qtMjFI86jlA
Practical Session
Video from the practical session:
https://youtube.com/shorts/uKRVOUrx3sM?feature=share
On the robot-laptop open rviz. Observe the laser data. How much noise is there on the laser? What objects can be seen by the laser? Which objects cannot? How do your own legs look like to the robot?
The laser can see obstacles that are on the same plane with the sensor. The noise is very small and when we compared a measurement with what we measured with a measurement tape we found the difference to be very small. The sensor has a range of 10 meters, so obstacles further away weren't visible in RVIZ. Furthermore the viewing angle is around 115 degrees from the front of the robot to the right and 115 degrees from the front to the left. That means if something is behind the robot, the robot can't see it. Our legs appear to be as half circular shapes, since the sensor detects only the legs and not the feet.
Take your example of don't crash and test it on the robot. Does it work like in simulation? Why? Why not? (choose the most promising version of don't crash that you have.)
The implementations which where checking for a single point in the laser ranges list didn't work that well because a leg or box might be in front of the robot while not getting hit by the laser ray at 0 degrees. Thus, we modified our code to detect the ranges in a specific angle (e.g. 30 degrees) and stop if it finds an obstacle close enough in these ranges.
If necessary make changes to your code and test again. What changes did you have to make? Why? Was this something you could have found in simulation?
After making the before mentioned change, the robot could detect obstacles that were in front of it even if we moved them a bit in any direction. That was something we couldn't see in the simulation since we didn't have dynamic obstacles or static small obstacles and the underlying problem wasn't visible when we were dealing only with walls.
Problem Statement
Local planning's job is finding what translational and rotational velocity to send to the robot's wheels controller given a "local" goal. The local goal in this context is usually some point on the global path which takes us from a starting position to a final destination. Local planning will usually account for live/active sensor readings, and is the algorithm most responsible for dynamic obstacle avoidance.. It will try to follow the global plan if given, but if a dynamic object is kept in the environment that the global planner did not account for, there is a high probability that the robot might crash into it. It is the job of a local planner to avoid such scenarios.
For local navigation, the two solutions we considered for the assignment are the Dynamic Window Approach and the Artificial Potential Fields.
Simulation
Dynamic Window Approach
We implemented the dynamic window approach algorithm based on the paper "The Dynamic Window Approach to Collision Avoidance", by D. Fox et al[1].
Implementation of code and functionality
The algorithm is implemented in the DWA.cpp file. The main function of the algorithm is the Velocity dwa_step(emc::PoseData current_pose, std::vector<Point2D>* point_cloud, Velocity robot_vel) which finds the the next best velocity based on the current pose (position and orientation) of the robot, the point cloud that represents the current LRF measurement and the current robot's velocity. The Velocity class represents a combination of translational and rotational velocity and the Point2D a two dimensional point with x and y coordinates. For the evaluation of the candidate velocities we use the following formula:
score = k_h*((M_PI-heading_error)/M_PI) + k_d*distance/big_const + k_s*vel.trans_vel/max_trans_vel
The three different components of the scoring function are normalized in the [0,1] range to allow better tuning of the scoring by the use of a coefficient for each component. We try to maximize the score, thus all the components are expressed in a way where the higher the value, the better. The components can be explained as follows:
heading_error- Given a candidate velocity, it represents the angle (the absolute value) between the direction towards the goal and robot's heading for its next position with the given velocity. The heading of the robot is represented in the range of [-pi,pi] and the heading error in the range of [0,pi]. It is calculated with the functionfloat calculateHeadingError(emc::PoseData next_pose, Point2D goal)where we calculate the next pose before calling the function given the candidate velocity combination.distance- Given a candidate velocity, the robot's current pose and a point cloud generated from the current LRF measurement, it represents the distance that the robot would need to travel with the candidate velocity to end up colliding with an obstacle. This distance is sometimes referred as the clearance for the candidate velocity. The algorithm has a parameter for how many points to look ahead, where each point is dt=1/frequency seconds away from the previous one. A point of the point cloud is considered to cause a collision with the robot at a projected position if it is inside a circle centered at the projected position with radius equal to a predefined clearance radius. The distance value is calculated with thedouble calculateDistanceFromCollision(std::vector<Point2D>* points, emc::PoseData current_pose, Velocity vel)function.trans_vel- It represents a candidate velocity's translational magnitude. The purpose here is to motivate the robot to move further away if the other components don't get affected.
The tuning of the coefficients for each component of the scoring function wasn't trivial since different relations between the coefficients result in different behaviors. For example, a lower coefficient for the heading component together with a higher one for the clearance score, will result in more exploration of the space where the robot prefers to move towards the empty space instead of moving to the goal. If have the reversed relation the robot would prefer to move towards the goal but in the case of a dynamic obstacle in between, it wouldn't move away from the obstacle since that would also make it move away from the goal.
Simulation Results
Video displaying the run on the simulation environment:
https://www.youtube.com/watch?v=v6rQc6_jtUE
Artificial Potential Fields
Implementation of code and functionality
The Artificial Potential Fields method is implemented with the lecture slides as a basis. In the theory, a potential can be calculated at every point the robot can be in. The potential consist of an attracting component based on the goal. Being further from the goal means a higher potential. The potential increases as well when coming closer to unwanted object, which acts as a repelling force. When taking the derivative of this potential field, an artificial force can be derived to push the robot towards the goal while avoiding obstacles.
Implementing the theory in the code requires a different approach to the same concept. The robot needs to base the potentials on sensor data instead of a known map. To accomplish this the potential is calculated for multiple locations around the robot with shifted sensor data, essentially predicting the potential at multiple possible locations. All LiDAR points induce a reppelling potential, normalised for the amount of read LiDAR points. For the direction in which the difference with the current potential is the highest, the artificial force is used. The artificial force is scaled and directly implemented in the desired robot velocity and rotation. After conducting experiments, the speed/force had to be capped to increase robustness and to keep up with the LiDAR refresh rate.
Simulation Results
Video displaying the simulation results: https://youtu.be/aqUUIiQzgVs.
Problems
Map 3 and 4 do not work with the Artificial Potential Field due to the presence of local minima in the artificial field. It is expected the global planner will solve this problem when having enough nodes. If this is not the case, a solution has to be found.
Assignment Questions
1. What are the advantages and disadvantages of your solutions?
For the DWA algorithm the main advantage is that the robot can dynamically avoid unexpected obstacles provided that they are not forming a dead end. The main disadvantage is the conceptual and computational complexity, which made us lower the frequency of the algorithm and make its decision space more sparse. Another disadvantage is the unavoidable trade off between the heading towards the goal and the dynamic obstacle avoidance.
For the Artificial Potential Field method the advantages are the robust and easily tunable parameters, together with the fact the method is computationally cheap. The downside is the presence of local minima. The robot can get stuck when moving in such local minima. Additionally, there is always a force acting on the robot. This means the robot always wants to move, even when it might not be beneficial in for example the restaurant challenge scenario.
2. What are possible scenarios which can result in failures for each implementation?
For DWA a dead end after which the goal is located, would cause the robot to end up in a position where heading towards any direction would make it head away from the goal and eventually move towards one the two walls of the dead end. Lowering the heading coefficient even further could make the robot travel back towards the empty space but then the robot wouldn't move towards the goal even when if it could because the heading wouldn't be affecting the scoring function that much.
For the Artificial Potential Field method, the failure scenarios are identical to the previous mentioned disadvantages.
3. How would you prevent these scenarios from happening?
The above scenarios represent unavoidable local minima when we are using only a local planner. To handle this situation we are going to implement a global planner which will be able to provide us with a good path by avoiding dead ends and obstacles in the known map. However, dynamic obstacles could cause a local minimum. For the handling of such situations, we are planning to detect them and first try to rotate away from the obstacle and if that fails, let the global planner know that we couldn't reach this region and ask for a new path by taking into account the non reachable region. It is worth noting though that dynamic obstacles such as a walking human, might move away if we just wait for a bit, thus we are also planning to have a timer in our local minimum detection component which will trigger the global path re-generation only after remaining on a local minimum for a specific amount of time.
4. For the final challenge, you will have to link local and global navigation. The global planner will provide a list of (x, y) (or (x, y, θ) ) positions to visit. How could these two algorithms be combined?
It is necessary to combine global planning with local planning and get the final result. We first need to find the optimal path through global planning. Since these paths are defined as node data, we only need to set the coordinates of the next node in the optimal path as the destination coordinates of local planning, and the navigation between the two nodes is completely by local planning, so that the obstacle avoidance and local optimal speed and angular speed of local planning can be realized under the premise of the optimal global path.
Global path planning: The global planning algorithm generates an advanced path from the start location to the destination location. It uses a map of the environment to identify waypoints or nodes that the robot needs to access, which are represented by coordinates (x, y) or (x, y, θ). The global planner provides a list of waypoints that form paths in the environment.
Local path planning: The local planning algorithm handles navigation between continuous waypoints provided by the global planner. It focuses on real-time obstacle avoidance and subtle movement adjustments. Local planners use real-time sensor data (such as laser scanning, odometer data) to detect and avoid obstacles, ensuring safe navigation between waypoints.
Combine global and local navigation: The global planner outputs a list of waypoints from which the local planner selects the next waypoint as the current destination. The local planner constantly navigates to the current waypoint, adjusting the path based on sensor data to avoid obstacles and ensure smooth movement. When the robot reaches the current waypoint (within the specified tolerance range), the local planner updates the current destination to the next waypoint in the global planner list. This process continues in cycles until the robot reaches the final goal specified by the global planner.
The specific steps are as follows:
1, Initialize global and local planners: Set up the global planner to calculate the initial path and initialize the local planner to handle real-time navigation.
2, Generate Global paths: Use the global planner to generate a sequence of waypoints (global paths) from the start location to the destination location.
3, Navigation with local planner: The first waypoint in the global path is set as the target of the local planner, and the local planner moves to the waypoint, using sensor data to avoid obstacles in real time.
4, Waypoint arrival check: Continuously check whether the robot has reached the current waypoint within the tolerance range. If arrived, the destination of the local planner is updated to the next waypoint in the global path.
5, Repeat: Repeat the process of navigating to the next waypoint and updating the target until you reach the final waypoint (the target location).
6, Dynamic change processing: If dynamic changes in the environment (such as unexpected obstacles) are detected, the local planner adjusts the path in real time. If necessary, a reassessment of the global path can be triggered to deal with significant deviations from the planned path.
With this approach, robots can effectively utilize global planning to plot paths in the environment and local planning to handle real-time navigation challenges between waypoints, ensuring efficient and safe movement to the final goal.
Practical Session
Dynamic Window Approach
When we run our code on the actual robot we noticed a similar to the simulation behavior. The robot would get stuck in local minima points for high values of the heading coefficient and for smaller values it would prefer to avoid the obstacles instead of heading towards the goal. We also noticed an oscillating behavior when no obstacles were near the robot and the robot was moving towards the goal. We initially believed that this behavior was caused due to the discretization of the possible heading directions. More specifically when the scoring function is only affected by the heading (e.g. no obstacles near the robot) the robot wants to have the perfect heading (zero heading error) towards the goal. However this isn't possible because we have discrete headings where none of them would be perfect for any given time. As a result, the robot picks once a non perfect heading which will cause a small divergence (heading error) and then it will pick a heading to fix this divergence which will have the same effect but now on the other side. That creates what we see as an oscillating path towards the goal. However after examining the code and working again with the real robot we found out that this was caused by a bug in the DWA code. In particular the error had to do with when the robot decides its next speed and when it actually sends that speed to the speed controller. Initially, we were first calculating the next best velocity and we were sending it to the robot after sleeping the needed time to keep to loop frequency. That created a lag between the speed decision and its application to the motors which resulted in the oscillating behavior. Apart from that, we made the function which calculates the distance to collision for the projected points more efficient by skipping unnecessary calculations.
Video of the practical session test:
Artificial Potential Field Approach
Video of the practical session tests: https://youtu.be/0HrUQvFmpbw.
Note the speed is capped compared to the simulation results in order to increase robustness and to keep up with the LiDAR refresh rate.
The algorithm worked quite well and the robot was able to reach the destination without any notable errors.
Problem Statement
As we know that the goal of the robot is to navigate through a map from a starting point to an end point on the map. But how will a robot navigate efficiently in the environment and dodging any know obstacles? This is where global navigation takes charge. It basically provides a systematic path to the robot which it can follow to reach the destination. There are multiple ways to implement global navigation but the team decided to use PRM and A* algorithms.
Simulation
Probabilistic Road Map (PRM)
Implementation and Code Exercises Explanation
Probabilistic Road Mapping is a technique used to create a path using nodes/vertices and edges/connections. To understand the implementation in detail, you can look at the code at our gitlab page. In brief, we start by randomly sampling the nodes in a map and connect every node in the proximity using an edge if they are valid. There are various advantages in using PRM algorithm as compared to grid based approach due to its flexibility and scalability. In the code, we used Bresenham's line algorithm that creates edges optimally that avoids all the existing know obstacles in the map. PRM uses navigation techniques like Dijkstra or A* algorithms to find the most efficient path in the graph generated by it.
The exercise algorithm implementation is explained as follow:
- For inflating the walls using the function
inflatedWalls, we first invert the colours usingbitwise_notand then create a kernel for dilation operation, which is used to inflate the walls of the map. The kernel's size is calculated based on the robot's radius and the resolution. The dilation operation adds pixels to the boundaries of the objects in an image. When we tried dilation without inverting the colours, the walls remained unchanged, instead the free space got affected. In order, to inflate the black walls, we have to invert the colours before and after applying thebitwise_notoperation.
- The
checkIfVertexIsValidmethod checks if the a new vertex is a valid vertex added to the map. It iterates over all existing vertices and calculates distances between each existing and new vertex. If the distance is less the the minimum threshold (min_edge_dist) that is set to 0.2, the new vertex is considered too close to the existing vertex. It returns a an appropriate flag according to the both situations. - The
checkIfVerticesAreClosemethod checks if the distance between the two vertices is less than or equal to the maximum threshold (max_edge_dist) of 1.0. This checks if the edge between the any two vertices are close i.e. the edge does not cross an obstacle and is within certain distance from other vertices. - The
checkIfEdgeCrossesObstaclefunction checks if an edge between two vertices crosses an obstacle. It first converts the vertices to map coordinates. The is uses Bresenham's line algorithm [2] to iterate over the edges. If any point crosses an obstacle (determined by checking if the values at the point in the map is less than the given threshold), the function returns the true flag indicate that the edge crosses an obstacle.
Advantages and Disadvantages
Advantages:
PRM is a very effective path generating algorithm as compared to grid based approach and other conventional path generating algorithms.
- While both grid-based mapping and PRM are flexible enough to handle most simple maps, PRM provides a superior solution because the path pattern changes each time it is reset. This allows for the creation of a new path whenever a new obstacle is introduced or if the current path is not optimal.
- Unlike grid-based mapping, which may require reducing the grid size to navigate tight spaces, PRM performs effectively when nodes are sparse enough, facilitating the creation of an efficient path. In tight spaces, a grid-based approach can cause the robot to move between closely spaced nodes very slowly to not hit the wall and not progressing directly towards the final destination.
Disadvantages:
Although, PRM is a very effective graph generation algorithm, it has certain drawbacks.
- For example, the algorithm effectiveness is highly dependent on hyperparameters that we provide like number of nodes, the minimum distance between the two nodes that it needs to connect, etc.
- While PRM is probabilistically complete (meaning it will find a path if one exists, given infinite time and samples), in practice, there is no guarantee it will find a path within a reasonable amount of time or with a finite number of samples, particularly in challenging environments.
- To make a smoother path, we need to increase the number of nodes, which in turn increases the complexity, resources and higher probability of failure in certain cases.
Simulation Results
Results: The PRM result for the given map_compare is the given image above.
Problems
Though PRM is an effective method to generate path, it poses certain problems.
1. There is a trade-off between the number of nodes and number of edges that we can create. Fewer nodes and edges can result in sparse roadmap resulting in poor coverage especially in complex environments or those with narrow passages, leading to missed paths or inefficient routes. Whereas, more nodes and edges results in a dense roadmap resulting in higher computational and memory costs, longer time to construct and query, and potential over-complexity.
2. Denser roadmaps also results in a higher probability of missing a target node when combined with local navigation testing in real life with Hero. The robot might miss a target node in order to avoid a dynamic obstacle. This is not good as the robot might try to reset the navigation path again and again in order to find the target node while avoiding the dynamic obstacle and try to reach the target node that might be occupied by the obstacle itself, resulting in failure to reach the goal.
Proposed Solution - A solution to deal with these drawbacks is to apply PRM* algorithm, which essentially works similar to RRT* but it can also give smoother navigation path in open spaces as it plots the nodes dynamically according to the free space in the map. So in tight spaces, the nodes will almost be simalar to PRM but now we can reduce the number of nodes (sparse). This will reduce the probabily of a node being occupied by a dynamic obstacle, hence improving the path planning and successfully reaching the goal.
I tried applying PRM* algorithm (can be found in PRM_star branch), but due to lack of time, we could not test it. Also, there were certain issues while debugging which might again require some time to fix.
A-star Algorithm
Implementation and Code Exercises Explanation
The basic algorithm of A-star is listed below:
- Set two empty node lists,
open_nodesandclosed_nodes. The OPEN list keeps track of those nodes that need to be examined; the CLOSED list keeps track of nodes that have already been examined(no need to take care anymore).
- Set three functions:
_nodelist[nodeID].gg(n) = the cost of getting from the initial node to n._nodelist[nodeID].hh(n) = heuristic function, the estimation of the cost of getting from n to the goal node._nodelist[nodeID].ff(n) = g(n) + h(n). the estimate of the best solution that goes through n.
- Introduce parent node: The node which is a predecessor of current node (on the optimal path from start node to curretn node) is known as a parent node. Each node also maintains a pointer to its parent.
The main algorithm follow below steps:
- Add
_start_nodeIDto the OPEN list. - Repeat following steps:
- Get node n off the
open_nodeswith the lowest f(n). Add n to theclosed_nodes. - For every neighbour nodes of current node
current_nodeID, e.g.for (int neighbourID : neighbours):- If the neighbour node
_nodelist[neighbourID]is unreachable or it is already in theclosed_nodes, ignore that node. Otherwise, do the followings. - If the neighbour node is not in the OPEN list, then add it to the OPEN list. Set current node as neighbour node's parent.
_nodelist[neighbourID].parent_node_ID = current_nodeID;store g(n), h(n), f(n) of that neighbour node. - If the neighbour node is already in the OPEN list, check whether this path (directly from the current node to neighbour node) is better, using the g(n) value as a reference. A smaller g(n) value indicates that this is a better path. If yes, set current node as parent of that neighbour node, and recalculate its g(n) and f(n) .
- If the neighbour node
- IF n is
_goal_nodeID, which means we have found the solution; or failed to reach_goal_nodeID, andopen_nodesis empty, which means there is no path. Then stop searching.
- Get node n off the
- Save the path. From
_goal_nodeID, from every node to itsparent_node_ID, until you reach the start node.
Advantages and Disadvantages
Advantages:
- A-star can find the best path quickly, quicker than other algorithm such as Dijkstra.
- Compared to Dijkstra, A-star go through less nodes, thus the efficiency is high.
- The evaluation function
_nodelist[nodeID].fcan be easily modified, to suit the implementation better.
Disadvantages:
- A-star does not go through every feasible solution, so the result may not be global minimum/maximum. (can be improved by modifying heuristic function
_nodelist[nodeID].h) - For a node, when there are multiple minimum in of its neighbour nodes' evaluation function
_nodelist[neighbourID].f, A-star cannot ensure the final path is the best path. - Large amount of computation. the growth of nodes number will lead to geometric growth of computation. (Complexity = O(n^2 ∗ log(n)))
Problems
As mentioned above, the computational complexity can easily explode if node number increase. However, when using PRM to generate a better graph, more nodes is necessary. Otherwise, if node is too sparse, it is hard to generate the best path from given graph, and will be likely to not form a continuously path either. Thus, when combining PRM and A-star, there is a trade-off between node number and optimal path.
Combining local and global planning
The purpose of this code is to implement a mobile robot using dynamic window method (DWA) in the tasks of global path planning and real-time obstacle avoidance. First, the program loads a configuration file to determine which path planning mode to use (grid map or probabilistic roadmap) and performs path planning based on that configuration. The robot then follows the planned path. In the main cycle, the robot updates its current position and obstacle information by reading odometer and laser data. The DWA algorithm then computes the currently optimal speed instruction, allowing the robot to avoid obstacles and move to the next target point. This is done by calling the dwa_step function, which calculates the best line and angular velocity based on the current attitude, laser point cloud data, and target point. Finally, the program sends the calculated speed instructions to the robot to perform the actual move.
The program first loads path-planning parameters from the configuration file. Determine the configuration file path to use based on the command line parameters. If no configuration file path is provided, the default configuration file is used. Load the contents of the configuration file using the load_config_file(filename) function. Based on the content of the configuration file, the program determines which path planning mode to use: a grid map (MODE_GRIDMAP) or a probabilistic roadmap map (MODE_PRM). Based on the selected schema, the program builds the corresponding planner object and loads the corresponding map or graphical data. Use the built planner object to call the planPath() method for path planning. If the path is found, the program converts the ID of the path node to the actual coordinate point and prints the planned path.
Initializes the initial position and speed of the robot. Set the target points (extracted from the planned path points). Entering the main loop, the robot continuously performs the following steps: Reading the odometer data updates the current position. Calculate the error between the current position and the current target point. If the robot reaches the current target point, the next target point is updated. The laser data is read and generated into point cloud data, representing the surrounding obstacles. The DWA algorithm dwa_step is invoked to calculate the optimal motion velocity (linear velocity and angular velocity) according to the current attitude, point cloud data and target point. The calculated speed command is sent to the robot to control its actual movement.
The DWA algorithm implements obstacle avoidance and path following through the following steps: Velocity sampling: Sampling different linear and angular velocities in the space of possible velocities. Trajectory prediction: For each sampling speed, predict the trajectory of the robot in a short period of time. Collision detection: Check whether the predicted trajectory will collide with an obstacle. Target score: Calculate the score of each collision-free trajectory, which is determined by three factors: the distance between the end of the trajectory and the target point, the speed of the trajectory, and the safety of the trajectory. Select Optimal speed: Select the speed with the highest score as the current control command. Through these steps, the DWA algorithm implements real-time path following and obstacle avoidance, ensuring that the robot can avoid obstacles and advance to the target point during the movement.
To use our local planner with the global planning code we had to make some modifications on the implementation. Specifically we implemented the local planner as a class. The planner's parameters are now attributes of an object and the driver code (main) can now set these parameters and call the relevant methods. Also the velocities are now sent to the robot through the main file instead of sending them inside the planner's functions. The local planner's method that is used the most in the main code is the "local_planner_step" method which finds the next transnational and rotational velocities given the current robot pose, the robot dynamics, the next (local) goal and the laser measurements.
Video after the described changes:
Assignment Questions
1. How could finding the shortest path through the maze using the A* algorithm be made more efficient by placing the nodes differently? Why would this be more efficient?
There are several ways by which we can improve node placement for efficiency:
Adaptive node placement - As proposed earlier, through the technique of PRM*, we can adjust the node placement where the nodes will be sparse in open spaces and more complex in tight spaces. This will not only reduce the computational costs but also result in a more effective and smoother path.
Critical point node placement - By placing nodes at critical points such as corners, junctions, and along potential paths. This reduces the total number of nodes by focusing on essential locations that define the path.
Combination of grid and PRM - By using grid for search space to find the larger empty spaces for placing fewer nodes using PRM in those regions and more nodes in tight spaces or near obstacle. Thus the computational costs can be reduced as the algorithm will focus more on placing the nodes in tight spaces. Fewer nodes mean less memory required to store node information, making the algorithm more efficient in terms of memory usage, which is particularly beneficial in resource-constrained environments.
2. Would implementing PRM in a map like the maze be efficient?
PRM's random sampling approach can effectively explore complex and irregular environments, including mazes. It doesn't rely on a predefined grid, allowing it to potentially find paths through intricate spaces. If the maze represents a high-dimensional planning problem (e.g., a robot with many degrees of freedom), PRM's ability to handle high-dimensional configuration spaces is advantageous.
In contrast, finding the optimal number of nodes to be placed and threshold distance to connect two nodes can be complex. If the roadmap does not adequately connect different regions of the maze, the resulting path may be suboptimal or even infeasible. This requires careful tuning of the sampling and connection strategies.
3. What would change if the map suddenly changes (e.g. the map gets updated)?
If the map or environment suddenly changes (e.g., new obstacles are introduced, or existing obstacles are removed), the implementation of the PRM algorithm needs to adapt to these changes to ensure the robot can still find a valid and efficient path. Changes in the environment can cause previously connected regions of the roadmap to become disconnected or some nodes and edges in the roadmap may become invalid if they now collide with newly introduced obstacles.
By employing incremental updates, hybrid approaches, and robust design principles, PRM can effectively manage dynamic environments and ensure reliable path planning. Continuous environmental monitoring might also help in these situations where we use sensors to continuously monitor the environment and detect changes. This can trigger updates to the roadmap only when significant changes are detected. Then periodically re-evaluating the roadmap at set intervals might ensure that it remains valid and efficient in the face of sudden changes.
4. How did you connect the local and global planner?
In this code, we achieve a combination of the two by taking the path nodes generated by the global path planning algorithm one by one as the target points of the Dynamic Window Method (DWA) algorithm. First, the program uses a global path planning algorithm (such as the A* algorithm) to generate a global path from the start to the end point, and converts the coordinates of the path nodes into a sequence of coordinates of the target points. In the main loop, the robot reads the path nodes in turn, passing the current target point to the DWA algorithm.
Based on the current robot attitude, obstacle point cloud data generated by laser scanning, and the current target point, the DWA algorithm calculates the optimal motion speed instruction (linear speed and angular speed). The robot moves according to these instructions, and when it approaches the current target point, the program updates the next target point and continues to execute the DWA algorithm. In this way, the DWA algorithm implements obstacle avoidance and path following on a local scale, while the global path planning algorithm provides a global path to ensure that the robot can get from the starting point to the end point smoothly.
5. Test the combination of your local and global planner for a longer period of time on the real robot. What do you see that happens in terms of the calculated position of the robot? What is a way to solve this?
When we test the combination of the local and global planners we see that after some time and a few turns the robot thinks that it's in a different position from the one where it really is. This is expected since the robot localizes itself only by dead reckoning using the wheels' odometers and there is always some slippage between the wheels and the ground especially when we accelerate or de-accelerate a lot. We believe this issue could be solved by the simultaneous use of a localization algorithm which would compare the LRF measurements to the prior map knowledge and correct the dead reckoning position.
6. Run the A* algorithm using the gridmap (with the provided nodelist) and using the PRM. What do you observe? Comment on the advantage of using PRM in an open space.
The implementation result of a-star in gridmap is shown below:
Small_Maze: https://youtu.be/MarLBC3igVI
Large_Maze: https://youtu.be/C9wwy7IZU4Y
After combining A-star and PRM, global navigation result in Compare_Map is shown: https://youtu.be/jQf0NvlVsYE
Also this video (a-star+ PRM, but with higher nodes number): https://youtu.be/1V__BW8XyRE
For the implementation without PRM, it can been observed that a blue line go through every nodes in path_node_IDs in order, and the robot follow exactly on the blue line, from _start_nodeID to _goal_nodeID given in json file.
For the implementation with PRM, it can been observed that a figure of comapre_map is generate. The figure is generate with PRM, showing nodes and edges on the open space of map(white area). Then same process as implementation without PRM, a blue line go through every nodes in past path, and the robot follow the blue line.
One thing need to be mentioned for both case. The robot will follow exactly on the edge path, when it needs to turn, the robot will reach a node and stop moving and start rotatiing, then start another section of path.
Practical Session
After working with the real robot, we noticed some problems with the DWA local planner. More specifically the robot would crash if obstacles were too close to it and the robot wouldn't move if the frequency of the planner was high. By noticing this behavior we found and resolved some bugs related to DWA. The issue we need to solve now is the case of a dynamic obstacle that ends up exactly on a node position making a local goal not reachable.
Video of our first trial for the combination of local and global planners in the real robot: https://youtu.be/qZW3frcgIZg
We see that the robot doesn't move even when there is enough space on the front of it (when we placed the bag). This happens because the lidar is on the front of the robot instead of being in the middle like in the simulation and the robot thinks that the obstacles are closer than they really are.
Week 4 and 5 - Localization
Problem Statement
To follow a planned path, a robot must know its current location. When we compare the simulation to the real world testing, we find that the robot does not work accurately. There is always certain amount of difference in the readings and the behaviour our robot in real world due to slip or inaccurate readings by the sensors. Overtime, this difference can result in deviations in the location of the robot. Localization enables a robot to accurately determine its position within an environment. Knowing its exact location is essential for navigating from one point to another without colliding with obstacles or getting lost. Given that for our final challenge the robot would start in a small region close to an initial guess and that for the rest of its task it would just need to compensate for the above mentioned disturbances, we identify our localization task as a tracking task.
Assignment Questions
Assignment for first week
Assignment 0.1
How is the code is structured?
Particle.h is included in ParticleFilterBase.h, and the latter is included in ParticleFilter.h .
What is the difference between the ParticleFilter and ParticleFilterBase classes, and how are they related to each other?
The ParticleFilter class inherits from the ParticleFilterBase class and extends its functionality. ParticleFilterBase provides basic interfaces(initialise, update, etc), and ParticleFilter implements specific functions (uniform/gaussian distribution, particle propagrate, recaculate weight, ..etc).
How are the ParticleFilter and Particle class related to eachother?
The Particle class represents each single particle in the particle filter, including position, weight, likelihoods, propagate, etc. The ParticleFilter class is responsible for managing the entire particle filter, it It may call methods of the Particle class to propagate individual particles, compute likelihoods and weights.
Both the ParticleFilterBase and Particle classes implement a propagation method. What is the difference between the methods?
In Particle class, void propagateSample propagate the Particle based on the received odom information, at the particle level; In ParticleFilterBase, void propagateSample propagate particles based on their kinematics, the odometry information and random noise, It iterates every particles in the filter and use the propagate method of the Particle class to each single particle.
Assignment 1.1
What are the advantages/disadvantages of using the first constructor, what are the advantages/disadvantages of the second one?
The first constructor generates N uniformly distributed particles in the whole map, and the second constructor generates N normal distributed particles around the position of robot.
For the first one, spreading all over the map can discover whole map with low computational cost, thus avoid trapping in local-min/max point. But most particles are distrubuted at un-relavant place, and will cost a lot to calculate their Posterior probability.
For the second one, more particles are distributed in high-probability region, thus can increase accuracy. But it can be easily trapped in local extreme point. Besides, choosing variance can influence the result as well, so the choice should be proper.
In which cases would we use either of them?
In cases where initial position is known(such as "tracking"), normal distribution constructor is recommanded; in cases where initial position is unknown (such as "Global localization"), uniform distribution constructor is recommanded.
[screenshot] From screenshot we can see the red arrows(with x, y, direction) normally distributed around the position of robot.
Assignment 1.2
Interpret the resulting filter average. What does it resemble? Is the estimated robot pose correct? Why?
weightedPosition[0] += particle.getWeight() * particle.getPosition()[0];
weightedPosition[0] = weightedPosition[0]/total_weight;
The filter calculates an average weighted position(x, y, direction) of all the particles., returns to a position vector resembles to real robot's position.
The estimated result is close but not exactly as the real position.
Because the resample is not setted yet, so the estimate result depends on limited N particles, especially on several particles with high weight, thus introduce big error in estimate.
Imagine a case in which the filter average is inadequate for determining the robot position.
[screenshot]: same screenshot as above. From it we can see a big green arrow (x,y,direction) represent the average state (a.k.a. the result after filter).
Assignment 1.3
Why do we need to inject noise into the propagation when the received odometry information already has an unknown noise component?
Because the motion data estimation (how particles mimic the robot’s moves based on its motion data.) is not perfect (always associated with noise) , so we have to model the uncertainty (such as wheel slip, uneven terrain) in motion. Injecting noise ensures that the filter can handle the inherent uncertainty in robot motion. Considering the noise to the motion data is also important to ensure that there will be a wide range of positions to test
What happens when we stop here, and do not incorporate a correction step?
Without correction, weight of each particles will not change according to their similarity to the real position of the robot. Particles within the “correct” region will not have higher weights than those in other areas. if there is a correction step, particles with higher weights are more likely to be selected, and thus subset{bad particles} --> subset{good particles}.
Recording video of localization result: https://youtu.be/yGidSriYTFc
Assignment for second week
Assignment 2.1
What does each of the component of the measurement model represent, and why is each necessary?
The measuremntmodel method of a particle object calculates the likelihood of a single ray's measurement, given the prediction for that ray based on the particle's pose. The likelihood is derived using the formula:
p_tot = hit_prob*p_hit + short_prob*p_short + max_prob*p_max + rand_prob*p_rand
The components in the formula can be described as:
p_hit- It represents how likely is that the measurement is exactly what it should be (if the robot was at the particle's location and orientation). This probability is modeled with only the exponential part of a Gaussian distribution to ensure values in the range [0,1],p_hit = exp( -0.5 * pow(((data-prediction)/hit_sigma),2) ).p_short- It represents how likely is that the measurement corresponds to a dynamic obstacle which is closer than the one present in the map. For example, a specific ray for a specific particle might hit a wall at 3 meters based on the map, but in reality a human might be standing in between the robot and the wall, making the ray hit an obstacle at 0.5 meters instead of 3 meters. This component calculates how likely it is that we are currently in the previous situation and it is modeled with an exponential distribution where we predefine its maximum value for measurements close to zero. The probability decreases exponentially to zero for measurements close to the predicted measurement.p_max- It represents how likely is that a measurement corresponds to a ray hitting a black/non reflective surface or something transparent like glass. In this case we would get a maximum range measurement while the predicted measurement might be something completely different (e.g. wall at 0.5m but measurement is 10m due to non reflective wall). It has a value of 1 if the measurement corresponds to the maximum range and 0 in any other case.p_rand- It represents how likely is that a measurement is random (not related to the prediction) even if the robot has the same pose as the particle. This isn't expected to happen a lot that why it has a small constant value for all measurements smaller than the range maximum value.
With each particle having N >> 1 rays, and each likelihood belonging to [0, 1], where could you see an issue given your current implementation of the likelihood computation?
The computeLikelihood method of a particle object calls the measuremntmodel for each ray of the particle and the corresponding measurement and returns the total likelihood of the measurement for the particle. To calculate the combined probability we assume independence of rays and we define the combined likelihood as the product of all the likelihoods for the the particle's rays (combined_likelihood = p(z1)*p(z2)*p(z3)*...*p(zN), where N is the number of rays). For a particle with pose much different than the robot's pose that could end up in numerical instability since we will be multiplying a very small number with another very small number multiple times, reaching a point where the product cannot be represented by the initial data structure (e.g. double). However this is handled by c++ and when the number is too small to fit in a float or double variable, the variable is set to 0. Regarding the independence of rays assumption, we think it is a valid assumption since we are working with a very sub sampled measurement and the prediction corresponds to the sub sampled space. Specifically, the initial list of 1000 ranges becomes a list of 67 ranges where we can say that the measurements are not correlated. However, in the original dense list of ranges we would probably have a high correlation of a measurement with its neighbors.
Assignment 2.2
What are the benefits and disadvantages of both the multinomial resampling and the stratified resampling?
Multinomial resampling
This algorithm takes particles in a uniform way from the list of cumulative weights/likelihoods. Its main benefit is that it is easy to understand. The main disadvantage is that it causes high variance in the amount of times a particle is chosen, meaning some particles are repeated many times while other particles are not used a lot. This could result in a selection of particles that might not be able to describe the robot's pose good enough.
Stratified resampling
This algorithm splits the list of cumulative weights/likelihoods into equal parts/ranges which are called strata. Then in each strata we draw uniformly a sample of the corresponding particles. In this way, we still reproduce with higher probability the particles with bigger weights while making sure we will reproduce also particles with smaller weights. The result is a more diversified set of samples. Also since each time we are searching in a smaller list that corresponds to the strata instead of the initial list, the algorithm is computationally more efficient than the multinomial. For our application we can't really identify a disadvantage of stratified resampling. However, in general it could be hard to split samples into strata which could make the use of the multinomial algorithm a better choice.
Assignment 2.3
The parameters we tuned are the following:
Particles- We set the particles number to 500 since we could localize successfully with that amount of particles while the code was running fast enough.motion_forward_stdandmotion_turn_std- We set the propagation noise standard deviation to 10cm for translation and 5 degrees for rotation since we could localize with that noise and still diversify the particles while tracking our position.meas_dist_std- We set the LRF measurement noise level to 2cm since the sensor is very accurate and we don't expect larger deviations.Algorithm- We use the stratified resampling algorithm due to the before mentioned advantages.Scheme- We use the effectiveParticleThreshold to perform the resampling only when it is detected that just a few particles are affecting the most the average position of the filter.
We tested the localization algorithm by initializing the simulation and setting the uncertain odometry to true. Also we move the robot further away from its initial guess. After performing several runs we believe that our localization module is accurate and runs fast enough to be integrated with the rest of the modules for the final challenge.
A video that demonstrates a run in the simulation with uncertain odometry:
Video demonstrating a difficult scenario for localization because there exists a large rectangular dynamic obstacle that makes the measurements very similar to the predicted ones for a position close to the obstacle, making the particle filter converge to the wrong estimate:
Final Challenge : Hero, the new age waiter
Videos of the final challenge
- The video of the designed system running on the real robot during the final challenge on 21 June 2024: https://youtu.be/ncUWcO743BM (3rd attempt)
- The video of initial attempts for the designed system for final challenge: https://youtu.be/-lya73TgR88 (1st and 2nd attempt)
- Simulation Testing video on the final challenge RestaurantMap2024: https://youtu.be/VLNTw9IdH2I
- Simulation Testing video on the final challenge RestaurantMap2024 with Variations and Moving Obstacles: https://youtu.be/_71ev8N3lXI
Introduction
In this challenge, Hero the robot is tasked with delivering orders in a dynamic restaurant environment. The goal is to navigate from the kitchen (starting point) to specified tables, as determined by the judges right before the challenge begins. Hero must contend with various static and dynamic obstacles, including chairs and human actors, to successfully deliver the orders. The robot must approach each table, signal its arrival with a sound, that signifies the order is delivered comfortably to the customer. This involves precise navigation and obstacle avoidance, using LiDAR for object detection and the provided environment map. The challenge tests not only Hero's ability to follow instructions and reach designated locations but also its capacity to adapt to an ever-changing environment, making it a true test of advanced robotics and autonomous navigation.
Prerequisites
There are certain requirements from each stakeholders' perspective that is expected from the robot Hero to fulfil in order to successfully complete the entire challenge:
- From customer point of view -
- The robot must use speech to communicate with customers, including phrases when it reaches a table or when it planning a route towards a new table from there. This ensures customer safety and overall a better service.
- Then the robot must approach the table, orient towards it, and move close enough for customers to comfortably take their order.
- It should be able to find an empty spot at the table and reposition if the initial spot is occupied.
- From Restaurant staff point of view -
- It should be reliable in all stages of operation, including localization, local planning, and global planning.
- The robot must have robust obstacle avoidance to ensure the safety of the restaurant staff, preventing collisions at all cost.
- There should be simple Table Number input Mechanism, allowing staff to easily input table numbers and manage orders.
- From software developer point of view -
- The robot should have modular code design for seamless integration of various components. By creating different cases of scenarios in the software architecture, ensures distinctive modules/components are separated from one another ensuring software readability and the ease for developers to easily pin-point flaws in a specific components.
- By making a config file which allows developers and operators to easily adjust all the parameters without altering the core code, ensures optimal performance in various settings.
- Restaurant staff or robot operators, who may not have a technical background, can still make necessary adjustments to the robot’s behavior through a simple config file.
Use this part for make intro for system architecture
System Design - Data Flow
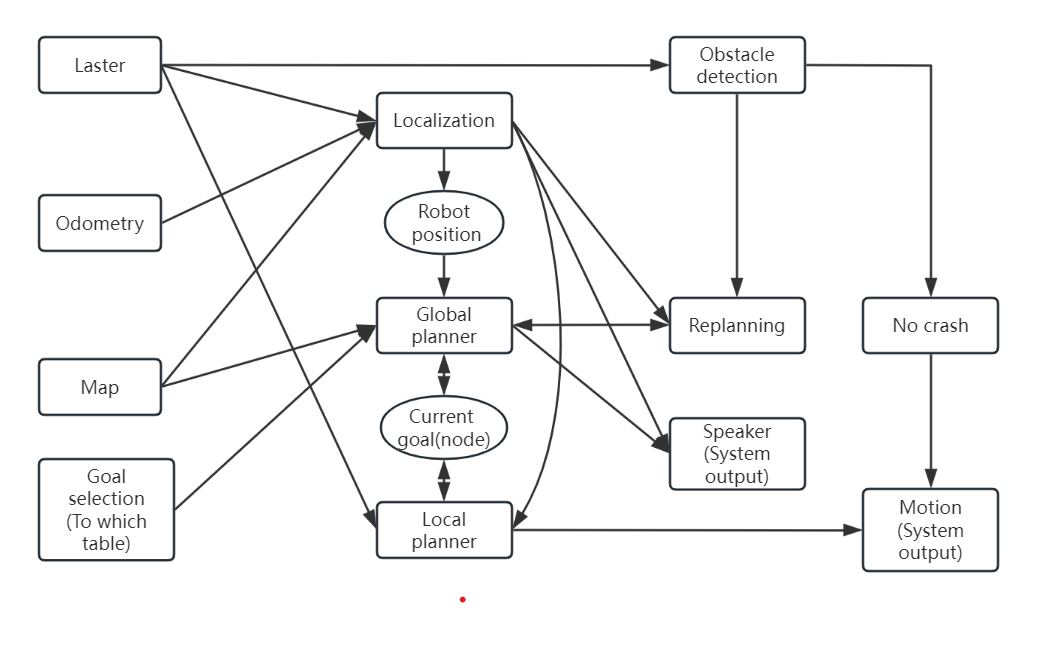
This diagram details the interactions and information flow between various modules. Firstly, the Laser sensor (Laster) provides obstacle information in the environment, and together with Odometry data, it inputs into the Localization Module to determine the robot's current position. The Map provides static information about the environment, and the Goal Selection Module determines the target location for the robot. This target is composed of table location information stored in the backend and the manually entered table visit sequence. Additionally, a dynamic planning algorithm ensures that the robot always selects the closest edge of the table as the global planning target point, and if this point is blocked, a new point will be replanned.
Based on these input data, the localization module calculates the robot's current position and transmits it to the Global Planner. The Global Planner module uses the current position and map information to generate a global path through the PRM algorithm and updates the Current Goal Node. The Local Planner dynamically plans the trajectory between the current position and the current goal node by comparing their information in real-time and formulates specific motion commands. At the same time, if it encounters any unknown obstacles, it will attempt to bypass them using local planner module. If the obstacle cannot be bypassed or is located at the next node, it will report an error message to the global planner and replan the path.
The Obstacle Detection Module utilizes laser sensor data to detect obstacles ahead in real time. Once an obstacle is detected within 0.2 meters, the no-crash protector (No crash) will trigger, causing the robot to stop immediately. If the obstacle is not removed within a long time, the Replanning Module will be triggered, reporting the current obstacle location to the global planner and updating the path through PRM again to ensure the robot's adaptability to the environment. Additionally, the system is equipped with a speaker module (Speaker (System output)) to provide voice feedback, informing users of the current system status or warning messages. After initialization, the localization module will send a message to the speaker to inform users that the initialization is complete. Throughout the process, the modules collaborate to ensure the robot safely reaches its intended destination according to the planned path.
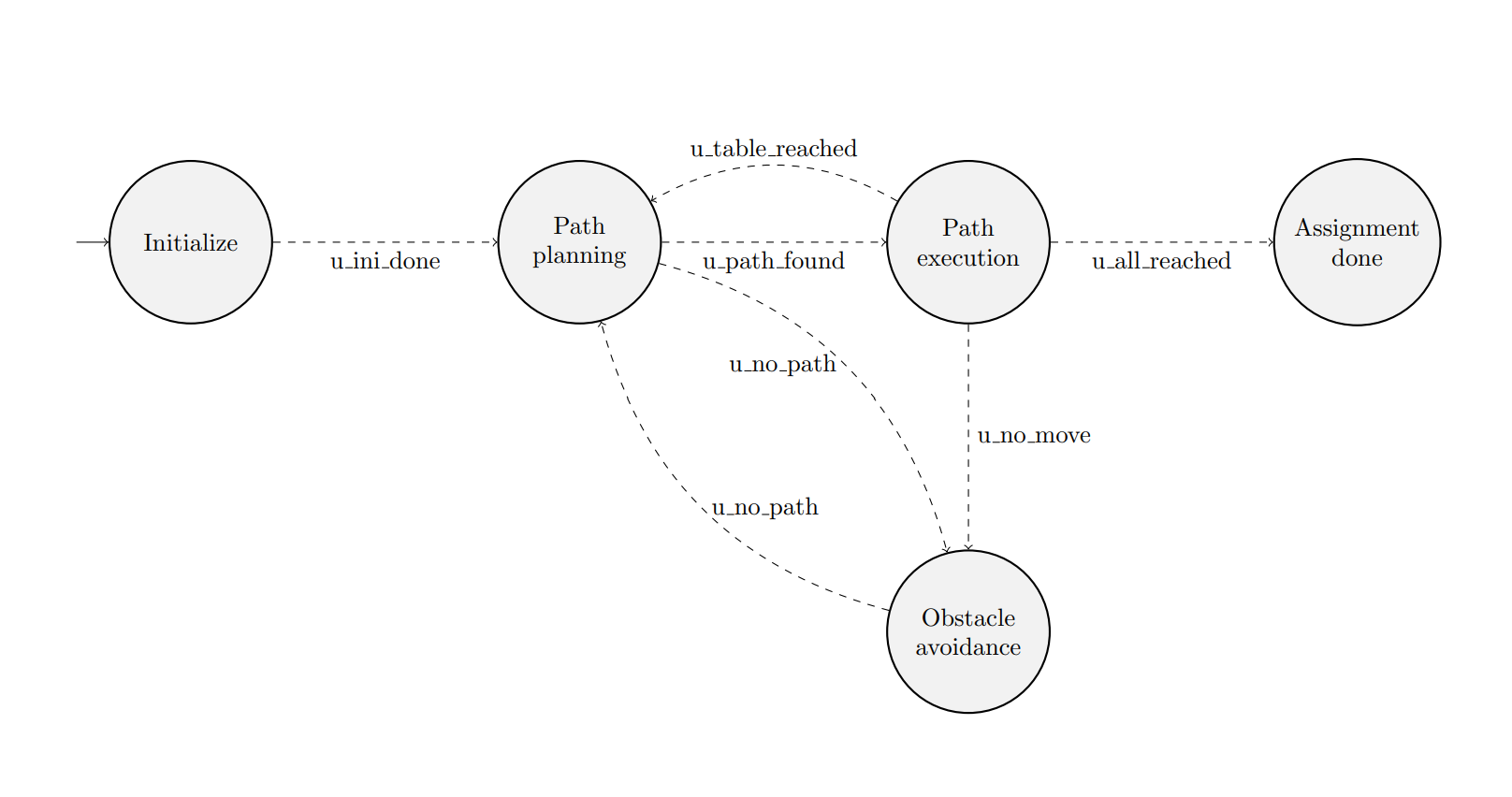
System Architecture
The robot is controlled by a supervisor class in C++ called "Robot." This class is initialized in the main script "main.cpp." Before it can be initialized, the "World" class and the "ParticleFilterBase" class need to be initialized. The "ParticleFilterBase" class was created in assignment four and is responsible for the localization of the robot in the space. The same applies to "World," which places the sensor data and the robot itself in a world model. The "World" class is used by both "Robot" and "ParticleFilterBase." Both classes are used by "Robot" as pointers. Other relevant classes used by the robot include "DWA" for the local planner based on the Dynamic Window Approach, "Planner" for the global planner, and "PRM" for creating the PRM map. Additionally, "ParticleFilterBase" uses some additional classes. All relevant tuning parameters for all used classes and subclasses are dynamically loaded from a general config file for the robot. This allows for dynamic adjustment of parameters without recompiling the program. For example, adjusting the number of nodes for "PRM" or the clearance radius for "DWA."
Once the aforementioned initialization of the classes is completed, a while loop is started that continues running as long as there is an active IO connection with the robot. Each time the while loop is called, the function "handle_current_state()" is invoked. This function ensures that the state function that is currently active is called. Each state has its own state ID. The ID of the currently active state is stored in the "Robot" class. A switch function is used to call the correct function corresponding to a state ID. After executing the state function, several conditions are checked that could result in changing the state and thus the state ID. For instance, if the robot reaches the last node of the planned global path, a new path needs to be planned. The possible transitions from state to state and the states themselves will be further explained below. Additionally, the state diagram is shown. The robot announces each transition.
The "Robot" class contains the following states:
Initialization - Robot::state_initialize()
Although the "Robot" class is initialized, more needs to be done before the robot is ready to depart for the first table. The robot must converge from the initial guess positions to the actual position of the robot. To do this, the robot rotates completely around its axis while making small forward and backward movements. Practical tests have shown that this best converges to the actual location. Before this can happen, the laser data in the "World" class must be initialized.
From this state, it can transition to the "Path planning" state once the robot has completed one full rotation. In hindsight, it would have been better to add an extra condition here, namely checking whether the localized position is close enough to the initial guess.
Path planning - Robot::state_set_goal()
Before the robot can depart for a goal or table, a path to this table must be planned. When the "Robot" class is initialized, a PRM map is created. In this state, only the nodes in the quadrant where the goal is located relative to the robot in the world frame are considered. The node closest to the robot is designated as the start node. The node closest to the table relative to the current robot location is chosen as the end node. When a path is found by the "Planner" class, the robot can move towards its goal.
From this state, it can transition to the "Path execution" state if a path is found. If no path can be found, it can transition to the "Obstacle avoidance" state to find an alternative path. The robot saves the distance travelled for a set amount of past cycles. When the mean distance travelled becomes lower than a set threshold, the robot goes to the state "Obstacle avoidance".
Path execution - Robot::state_goto_goal()
The robot moves according to the nodes given by the "Planner." Each time the state is called from the main loop, localization is attempted if the sensor data for odometry and LiDAR are available. The average position is requested from "ParticleFilterBase," which "DWA" then uses to calculate the next step. When an intermediate node is reached, this node is removed from the list of coordinates to be visited.
When all intermediate nodes are visited, it means that the final goal is reached. If not all tables have been visited, a new goal is sought through the "Path planning" state. Otherwise, it will transition to the "Assignment done" state.
Obstacle avoidance - Robot::state_add_obstacle()
Sometimes the robot may encounter an obstacle. When it is identified that the robot can no longer move to its next intended node, this state is activated. The "Planner" is called again to create a new path in the same manner as the "Set goal" state. The main difference is that a new map is created by the "PRM" class based on the LiDAR data. LiDAR data points within a configurable range of the robot. From these points, a configurable distance in the same direction as the robot is removed from the map as a navigable area. This area is then inflated as previously explained in assignment 3. The method to achieve this is by subtracting the created matte from the original map. This new map will be temporarily used by the "Planner" for an alternative path.
From this state, it can transition to the "Path execution" state if a path is found. If no path can be found, it can transition to the "Path planning" state to attempt regular path planning. [add picture of blocked path]
Assignment done - Robot::state_done()
Last state without any new possibilities for states. It is ensured that the robot will not move anymore in this state.
The following states are included in the initial state diagram but not implemented:
Waiting at door - Robot::state_wait_door()
The ideal situation here would be to add a penalty to the "Planner" class when the robot wants to go through the door. This way, it is not preferred to take the closed door if another route is better. If the route through the door must be taken, then LiDAR information can be used to recognize if the desired path is blocked. The robot will then wait until the LiDAR information recognizes a clear path in this state.
Delivering order - Robot::state_deliver_order()
In this state, the robot could deliver the order when a table is reached. It can do this by rotating to the table and waiting for a set amount of time. It is possible to move towards the table if that helps the people at the table to take the food.
The individual components were adapted according to the needs of the final challenge and are explained as follows:
Intialization
The local planning phase is critical for ensuring that the robot, Hero, successfully navigates the dynamic restaurant environment while delivering orders to designated tables. During this phase, Hero uses the Dynamic Window Approach (DWA) to handle real-time path planning and obstacle avoidance. Key parameters for the DWA, such as translational and rotational velocities, acceleration limits, and clearance radius, are configured through a flexible settings config file to adapt to varying restaurant conditions.
The robot continuously samples a range of possible translational and rotational velocities, simulating short-term trajectories for each pair. These trajectories are evaluated based on their alignment with the goal, the distance to the nearest obstacle, and the robot's forward speed. By scoring each trajectory using a weighted objective function and selecting the highest-scoring velocity, DWA ensures that the robot maintains an optimal path. This process repeats in a loop, allowing the robot to adapt to changes in the environment, such as moving obstacles or shifts in the goal position. Consequently, DWA's ability to dynamically adjust the robot's path based on real-time sensor data ensures efficient and safe navigation, crucial for the complexities of the final challenge. When a goal node is successfully reached, the robot updates its current position and this is done after each step of dwa as explained in assignment 2 until the loop ends or replanning is triggered.
Obstacle avoidance is a key feature of the local planner, allowing Hero to detect and maneuver around static and dynamic obstacles, such as furniture and moving human actors, without collisions. This is achieved by continuously updating its environment model using LiDAR scans and odometry data. When an obstacle is detected within a predefined clearance radius in the config file, the robot dynamically recalculates its path to ensure a safe and smooth trajectory towards its goal. Path following is managed by setting sequential waypoints derived from a pre-planned global path. As Hero progresses, it adjusts its motion to stay on course towards the current waypoint. Upon reaching each waypoint, the robot reorients towards the next until it arrives near the target table. Once it reaches a table, Hero announces its arrival with a clear audio signal, ensuring a seamless and polite interaction with the customers. If an occupied spot is encountered, it calls the replanning module which generates an alternative path for docking around the table.
For global planning, the PRM (Probabilistic Roadmap) code from the project was utilized. Due to the requirement to visit each table sequentially, a single PRM planning is conducted for global planning, and the A* algorithm is employed for path planning each time a table is visited. Based on the simulated map data, the resolution of PRM is set to 0.025 pixels. To ensure that nodes are not generated between two tables (since the robot's width cannot fit between tables, making those nodes unreachable), the wall expansion coefficient is set to 0.58, thus preventing the generation of nodes too close to any surface. Additionally, we need to adjust the grayscale recognition to ensure that gray doors are not identified as walls, thereby allowing paths that pass through doors to be generated.To enhance the stability of the PRM algorithm, additional algorithms were incorporated to increase the number of nodes generated around tables. This ensures that even if one or several nodes are occupied, alternative nodes can still serve as endpoints near the tables.
To ensure that the robot can be controlled to visit tables in a specified order by inputting table numbers, the coordinates of the four corners of each table are stored in a configuration file. An algorithm matches the table numbers to their respective coordinates, ensuring that the table coordinates can be directly recognized. In the goal selection algorithm, the input number is first mapped to the corresponding table coordinates. Then, the algorithm searches for PRM-generated nodes near the table and selects the node closest to the current starting point as the target point as mentioned in path planning state.
In practical operation, the robot first initializes and confirms its current coordinates. After the path is generated and the final goal that is the first table is reached, the robot re-plans the path using its current coordinates as the new starting point and the next goal as the endpoint. This process continues iteratively until the robot reaches the final goal. This approach allows for the dynamic switching of goals and robust path planning by incorporating Localization, thereby avoiding errors that could arise from using the previous endpoint's coordinates as the new starting point.
Replanning
In path replanning, we need to consider two scenarios. The first scenario occurs when there is an obstacle on the current path. According to DWA settings, if the next node is occupied by an obstacle, the robot will stop until the node becomes available. But if it does not move, the robot will stay there indefinitely. To avoid this situation, it is necessary to replan a path around the obstacle while maintaining the same goal. The second scenario arises when the goal node neat the table is occupied or there is an obstacle nearby, preventing access to the intended goal. In this case, a new goal must be selected to conclude the current path planning.
To determine the need for replanning, we integrate data from the laser sensor. When the laser sensor detects an obstacle ahead that impedes movement, we read the sensor data to calculate the obstacle's width. By combining the obstacle's width with the global planning node information, we assess whether the obstacle obstructs subsequent paths. If the subsequent nodes are deemed inaccessible, path replanning is initiated; otherwise, the obstacle is simply bypassed. Additionally, we monitor the robot's speed. If the robot's speed is zero for more than 10 seconds, the system will trigger replanning. For scenarios where the goal node is inaccessible, the laser sensor detects if the goal node is occupied and compares the robot's current coordinates with the goal coordinates. If the sensor data indicates that the current distance to the node is greater than the distance to the obstacle, the goal replanning process is initiated.
During path replanning, the first step involves measuring the obstacle's width using the laser sensor and constructing a rectangle in the PRM map with a side length equal to the measured width. The starting edge of the rectangle is the distance detected from the obstacle. Using the robot's current coordinates and the distance measured by the laser sensor as references, we calculate the approximate position coordinates of the obstacle. Before running the PRM algorithm again, we update the simulated map to mark this area as an impassable region (displayed as a black area on the map). Then, the PRM algorithm is rerun to generate new paths and nodes, keeping the original goal node unchanged. Using the robot's current coordinates as the starting point, the A* algorithm is employed to replan the path.
For goal replanning, the steps are similar. The only difference is that after confirming the goal is obstructed, the goal selection algorithm is rerun to choose an alternative accessible node. If the path to this node is not obstructed, the goal is updated to this new node, and the A* algorithm is rerun to plan the path. If the path remains impassable, other nodes are selected until a feasible path is found. If all nodes are obstructed, the obstacle is marked, and the PRM is rerun.
The simulation video to display working of replanning can be found here: https://youtu.be/dWZ9Ip53ogI
Localization
The localization component is responsible for global localization during initialization and then tracking the robot's pose for the rest of the challenge. Before the robot starts moving towards a table, it performs a small circle around itself to make the particle filter's estimations converge to (hopefully) the robot's real position. For estimating the initial position of the robot, we use a guess inside the given starting area and more specifically "initial_guess": [1.5, 0.7, 1.57]. The inner workings of localization remain the same as in exercises apart from the a bug that was causing unexpected errors during runs on the real robot. Particularly, the problem was in the compute likelihood function of a particle where the combined probability of each particle's rays is calculated as a product of the individual probabilities. As it was already mentioned in the exercises, that product could end up so small that the likelihood would be truncated to zero. However, during the exercises we didn't notice how would that affect the rest of the code and specifically the normalization step of the probabilities before resampling. Since now some particles had zero probability, any number multiplied by their probability would result again in zero probability and after the normalization the cumulative sum of the probabilities would no longer add up to 1. That apart from essentially deleting some particles, created the unexpected errors during resampling since the resampling algorithm assumes a search space of [0,1] for the cumulative sum vector. To solve that issue, we modified the compute likelihood function of a particle to set the calculated probability to a predefined lower bound if the product is smaller than this bound.
To test the localization component, we used the real robot during practical sessions and teleop to move it. After verifying that things were working without dynamic obstacles, we started introducing obstacles that weren't present in the map. We noticed that the particle filter was affected a lot by that and we tuned the probability coefficients of the measurement model. In particular we tried to find a balance between the short probability, which accounts for unmodeled obstacles, and the hit probability, which makes correct measurements more important.
Serving Tables
There are 5 tables in the map, in each circle we set a table as the destination of global planning. According to the given svg map, we manually set the center point of each table, as shown below.
"tables":
[[ 75, 320], [ 75, 190], [310, 290], [185, 50], [365, 50]].
When robot is planning to reach table, PRM will be used to generate nodes. The code will go through all the nodes, only considering the nodes which stand in the rectangular(diagonal: current position, table centre),
if (not (min_x < node.x < max_x and min_y < node.y < max_y)) {
continue;
}
and find out the node which is the closest to the table centre, and set it to the goal node.
After reaching the goal node, the robot will tell people that it has arrived (io.speak("Table " + to_string(table_seq[cur_table]) + " reached, please pickup your food");). Then the robot will plann the way to next table.
A failure scenario identified during initial testing phase for final challenge was the lack of a clearly defined distance within which a robot is considered to be serving. Consequently, there is no specific limitation to control the distance between the goal node and the table center in the code. For instance, the code tends to select nodes located between tables 1 and 2 as the goal node (as shown in the red circle in the image, with an "infl_radius" of 0.58). However, this gap distance conflicts with the "dont_crash" code or "clearance_radius," causing the robot to stand still between the tables and fail to reach the goal node. Even if the robot reaches the goal node, it cannot move backward and needs a diameter to turn around. The narrow gap conflicts with the DWA algorithm, preventing the robot from exiting the gap. These problems can be resolved by increasing the inflation radius in the PRM, ensuring the gap between tables is filled, and no nodes are generated between the tables. However, increasing the inflation radius also increases the distance between the table and the robot's serving point.
An improvement done was that we choose the node closest to table edge instead of choosing the node closest to the table centre. In json file, tables are constructed by segments, and each segment of individual table is given by four points.
"tables":
[ [49, 50], [50, 41], [41, 40], [40, 49]],
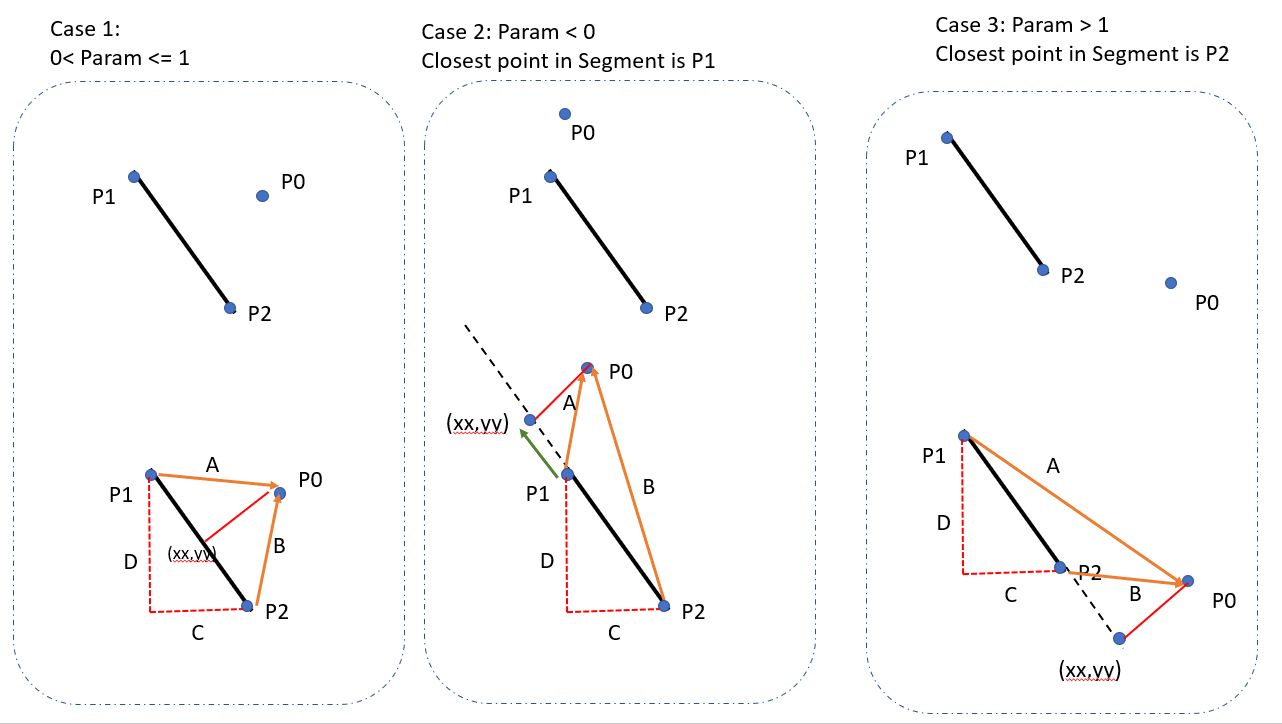
For example, in the new goal selection algorithms, it will go through all nodes, and find the node which is closest to any segment of the table, and set that node to the goal node of serving table.
But achieving this requires us to read and store of json file, and create different struct for points, segment, and table.
struct Point { double x; double y; };
struct Segment { Point start; Point end; };
struct Table { std::vector<Segment> segments; };
Opening the Door
To implement the task of opening a door for the final challenge, the code first retrieves the robot's current position with coordinates x and y. It then checks if the robot is near the door by using the `isNearDoor` function, with a distance threshold of 0.5 units. If the robot is within this threshold, it stops the robot by sending a base reference of (0, 0, 0) to halt its movement. The code then pauses the robot's activity for five seconds using `std::this_thread::sleep_for`. After the pause, the robot announces "open the door" using the `io.speak` function. Following this, the robot resumes its tasks by calculating the next step of its Dynamic Window Approach (DWA) algorithm using `lp.dwa_step`, which considers the current position and point cloud data. Finally, the new velocity commands are sent to the robot's base to continue its movement.
If the door does not open, the replanning will be triggered to find an alternative route towards the goal. Another thing to notice here is that, when the robot is trying to cross the door boundary, Localisation particles are seen to blow-up. This was a major problem because the robot is clueless when trying to pass through the door. Additionally, due to this, we can see that it takes a lot of time for the system to process this transition and eventually making the robot to move very very slowly through the door. This issue can also trigger unwanted replanning even if the door was opened and robot is passing safely through it.
The simulation video can be found here: https://youtu.be/J_RSyXLSdz4
Final Challenge Results
Final Results Videos can be found in the starting of the final challenge report.
First Two Tries
In our first tries the robot couldn't perform global localization and had a big offset between its real and its estimated position. After the final challenge, we examined the video and recreated the scenario in simulation. We noticed that even when the particle filter pose was close to the real pose, the particles were quite spread and they would converge to a small region only when the measurements were very close to the predictions (no unmodeled obstacles). Considering this, we realized that the lower bound we set for the combined likelihood was so small (1e-15) that in most of the real life cases the measurement model would return the lower bound value for the majority of particles. By modifying the lower bound to a much smaller value (1e-300) we didn't notice this undesired behavior any more.
The Third Try
Unfortunately, during the final challenge we thought that the particle filter wasn't working because of the coefficients used for each component of the measuremnt model. Thus we tried to increase the hit probability coefficient and decrease the short probability coefficient to make the filter converge to a position where the measurements will match more to the predictions. However, as mentioned in the previous section, the lower bound for the combined probability was too big. By starting the robot facing the empty space, we managed to localize (no shorter than predicted measurements) and the particle filter's pose estimate was close to the real position for most of the time. Although, the particles were quite spread and after introducing a lot of dynamic obstacles the estimate was getting again away from the real pose.
Regarding the navigation, when the robot was heading towards the (unmodeled) chair, it came as close as the clearance radius would allow and practically stop. This is a local minimum for the local planner where all the possible trajectories would be considered as non admissible trajectories (lead to collision) due to the very close distance from the obstacle. Then after replanning, the robot was still very close to the obstacle in front, making again any trajectory (with translation) non admissible. After many executions of the replanning, the next goal was more to the right of the robot instead of being in front which made the robot after turning towards the goal to also move since there were no longer obstacles in front. This could be easily resolved by a head away from obstacles procedure, where after replanning the robot would first turn until it reached an orientation with enough free space ahead and then try to go the next goal with the local planner.
Lastly, we didn't have the time to test planning by considering the doors and since it was our last try, the team decided to not implement it and for that reason the door was treated as a wall. Consequently, when the robot reached a situation where its way was blocked and the only possible path would be through the door, it just remained stationary since it couldn't find a possible path to its goal.
Improvements
This needs to be considered:
Exercises
- Can we see that you succesfully completed the exercises from your wiki page.
Component selection Restaurant challenge (Addy)
- Is the choice of components motivated by the challenge?
- Are the components adapted to the requirements of final challenge?
- Does the wiki show an understanding of the algorithms in the component?
Experimental validation of the components
- Are the components tested individually?
- Are the experiments performed a suitable approximation of the conditions of the final challenge?
- Are the conclusions drawn supported by the results of the experiments?
System design for the final challenge(Yuhui)
- Is the design presented complete?
- Is the design communicated clearly?
- Are design choices motivated by the final challenge?
Experimental validation of system design
- Are the experiments performed a suitable approximation of the final challenge?
- Are the conclusions drawn supported by the results of the experiments?
Evaluation Restaurant challenge
- Is the behaviour during the final challenge explained?
- Is this behaviour linked back to the designed system?
- If applicable, is an adjustment to the design proposed?
References
- ↑ "The Dynamic Window Approach to Collision Avoidance"(https://ieeexplore.ieee.org/iel1/100/12589/00580977.pdf?casa_token=Tj4RmTFS6ZcAAAAA:sn6rPHqH4Ua0BKFMomLqAtgriJWgWW-hFtL6dGcXgBACiAAH3tUIV8hrXihjSjhfu4kGtmmc)
- ↑ Implementation of the Bresenham's Algorithm on a Four-Legged Robot to Create a KRPAI Arena Map(https://ieeexplore.ieee.org/iel7/9702758/9702759/09702849.pdf?casa_token=OO_R7iGpXWIAAAAA:wmanlx5JmqPOll4KgkN7iq8Pg0F5NQyZNpO1H08AEKceFrPBR-K11xDM9lzpmYtPwZPoTFS4)
- ↑ Shortest distance between a point and a line segment https://i.sstatic.net/sXc2j.png